An international team of cosmologists, leaded by a researcher from Paris Observatory, has improved the theoretical pertinence of the Poincaré Dodecahedral Space (PDS) topology to explain some observations of the Cosmic Microwave Background (CMB). In parallel, another international team has analyzed with new techniques the last data obtained by the WMAP satellite and found a topological signal characteristic of the PDS geometry.
The last fifteen years have shown considerable growth in attempts to determine the global shape of the universe, i.e. not only the curvature of space but also its…
Mathematics
Forty years ago, mathematician Mark Kac asked the theoretical question, "Can one hear the shape of a drum?"
If drums of different shapes always produce their own unique sound spectrum, then it should be possible to identify the shape of a specific drum merely by studying its spectrum, thus "hearing" the drum's shape (a procedure analogous to spectroscopy, the way scientists detect the composition of a faraway star by studying its light spectrum).
But what if two drums of different shapes could emit exactly the same sound? If so, it would be impossible to work backward from the spectrum and…

Sports pundits across the country have been comparing the so-far unbeaten 2007 New England Patriots to the perfect 1972 Dolphins all year. A New York cardiologist has used the scientific statistics used in large-scale medical trials to determine which of the two teams is superior.
Using a format and approach typically reserved for the cardiovascular therapy studies he writes and reviews, Dr. Jonathan Sackner-Bernstein, a Food & Drug Administration advisor and the Chief Medical Officer at Clinilabs, a clinical research organization in New York, compares the 2007 New England Patriots and…

58132764
72645831
76125483
81274365
I first saw these numbers in the book “Fun with Mathematics” by Jerome S. Meyer, published in 1961. I have had them on my computer terminal at work for years. The first two numbers are my favorites, I have been waiting for inspiration or insight, I want these numbers to talk to me - but nothing. They both have four sets of two numbers that should be telling me something 58, 13/31, 27/72, 64, some simple idea of shape, form or pattern. Mathematics, after all, has been described as the study of all possible patterns, therefor I should be able to ask and…

Three-dimensional snowflakes can now be grown in a computer using a program developed by mathematicians at UC Davis and the University of Wisconsin-Madison.
No two snowflakes are truly alike, but they can be very similar to each other, said Janko Gravner, a mathematics professor at UC Davis. Why they are not more different from each other is a mystery, Gravner said. Being able to model the process might answer some of these questions.
Intricate, incredibly variable and beautiful, snowflakes have been puzzling mathematicians since at least 1611, when Johannes Kepler predicted that the six-…

Who needs a computer? Two theoretical physicists at Rensselaer Polytechnic Institute grabbed a piece of paper and described the motion of interstellar shock waves — violent events associated with the birth of stars and planets.
The mathematical solution developed by Wayne Roberge, lead author and professor of physics, applied physics, and astronomy at Rensselaer and his colleague, adjunct professor Glenn Ciolek, reveals the force and movement of shock waves in plasma, the neutral and charged matter that makes up the dilute “air” of space. Unlike many previous studies of its kind, the…

For centuries, human beings have been entranced by the captivating glimmer of the diamond. What accounts for the stunning beauty of this most precious gem?
As mathematician Toshikazu Sunada explains in an article in the Notices of the American Mathematical Society, some secrets of the diamond's beauty can be uncovered by a mathematical analysis of its microscopic crystal structure. It turns out that this structure has some very special, and especially symmetric, properties. In fact, as Sunada discovered, out of an infinite universe of mathematical crystals, only one other shares these…
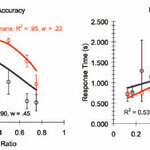
Adult humans possess some mathematical abilities that are unmatched by any other member of the animal kingdom but there is increasing evidence that the ability to count sets of objects nonverbally is a capacity that humans share with other animal species.
In PLoS Biology, Elizabeth Brannon and Jessica Cantlon discuss how humans and nonhuman animals share a capacity for nonverbal arithmetic. The researchers tested monkeys and college students on a nonverbal arithmetic task in which they had to add the numerical values of two sets of dots together and choose a stimulus from two options that…

The journal Experimental Mathematics, started in 1992, publishes “formal results inspired by experimentation, conjectures suggested by experiments, descriptions of algorithms and software for mathematical exploration, [and] surveys of areas of mathematics from the experimental point of view.” The founder wanted to make clearer and give more credit to an important way that mathematicians come up with new ideas. As the journal’s statement of philosophy puts it, “Experiment has always been, and increasingly is, an important method of mathematical discovery. (Gauss declared that his way of…

One of the foundations of Einstein's Special Relativity is that no particular frame of reference is better than any other - whether you're sitting on the couch or barreling through space on a rocket, physics doesn't change. On the other hand, as many physics undergrads learn, choosing the right reference frame can simplify your homework problems a lot.
Thanks to Einstein, physicists know that the world looks different depending on how fast you're moving. A new analysis shows that it is a lot prettier (mathematically speaking) if you're moving at just the right speed, leading to an improvement…