Have you ever looked at a histogram with the data displayed as counts per bin in the form of points with error bars, and wondered whether those fluctuations and departures from the underlying hypothesized model (usually overimposed as a continuous line or histogram) were really significant or worth ignoring ?
The subject is one of the topics which takes the most time away in discussions which arise during talks at internal meetings of HEP experiments. Physicists in the audience will be always happy to compare their ability of eye-fitting and to argue about whether there's a bump here or a mismodeling there. It is just as if we came with a built-in "goodness-of-fit" co-processor in the back of our mind, and that was connected with our mouth without passing through those other parts of our brain handling the "think first" commandment.
I am not overstating it: it happens day in and day out. For instance, it happened to a meeting I attended to yesterday. We were approving a physics result and somebody started arguing that most of the data points were above the fit in a certain region of the money plot of the analysis. This turned out to be false: in the specific case, the questioner was forgetting to take into account bins where the data had fluctuated down to zero entries, and the histogram had a logarithmic y scale (which made those points disappear from the horizon below the lower edge of the plot).
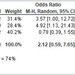
Besides the issue of deceiving zero-entry bins, there are several other reasons why one should be careful with such eyeballing comparisons, but by far the most important one is that the data, when they consist in event counts per bin, are universally shown as points with error bars, and the error bars by default are drawn symmetrically above and below the observed count, and extend from N - sqrt(N) to N + sqrt(N), if N is the bin content. In other words, the default is to assume that the event count, being a random variable drawn from a Poisson distribution, has a variance equal to the mean.
Here I should explain the least knowledgeable readers what is a Poisson distribution. Any statistics textbook explains that the Poisson is a discrete distribution describing the probability to observe N counts when an average of m is expected. Its formula, P(N|m)=[exp(-m)* m^N]/N! (where ! is the symbol for the factorial, such that N!=N*(N-1)*(N-2)*...*1, and P(N|m) should be read as "the probability that I observe N given an expectation value of m).