I am quite proud today to announce the publication of a new physics result from the CMS experiment: maybe not a groundbreaking result, yet one to which I contributed directly, and the first full-fledged analysis of CMS collider data brought to public domain by the group of Padova researchers to which I belong.
Two words on the CMS-Padova group
The group of physicists in Padova who are members of the CMS collaboration is quite large: in fact, it is the third-largest in CMS, and the largest University group, counting about 70 CMS collaborators (I believe we beat by a few units the fourth-largest group, Imperial College). Padova has contributed to the construction and installation of the inner silicon tracker, and had a major responsibility in the design, construction, and commissioning of the muon drift chambers.
The merging of the two teams, which had busied themselves for years in the arduous task of detector building and commissioning, into a strong analysis group has been slow and complicated. In the course of the last two years, as a co-chair of the CMS analysis group in Padova, I have tried to steer the quite varied physics interest of the many brilliant minds in my institute, to focus on few analysis topics to pursue actively and with a critical mass. This has proven hard for a while, because every thinking mind had his or her pet physics analysis in mind, and leaving your topic of choice alone to work on something else is never a simple decision.
Eventually, however, the data brought us together! As soon as the first proton-proton collisions became available, we successfully sought the signal of phi meson decays into kaon pairs -a decay of some interest to both the tracking and the muon detection souls of our group, since it will be in the near future a precise probe of the probability that charged kaons produce identified muons, by the mechanism which is colloquially called "punch-through".If you are searching for new physics with muons, you need to know very well how often you see punch-through muons coming from kaon decay.
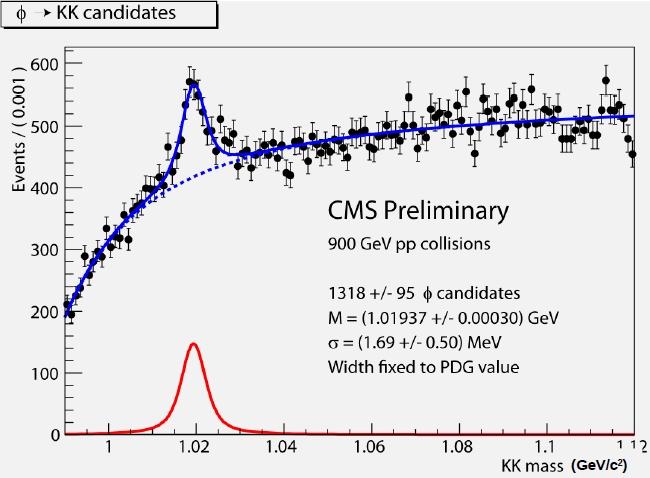In the matter of a couple of weeks, thanks primarily to the dedication of Luca (our pivot PhD student), Mario (a Post-Doc from Cyprus University who is actively collaborating with us), and Pierluigi (a undergraduate student), we got an approved result of phi decays, the bell-shaped bump you see in the picture on the left. But this was not really a "first physics result": it was just an appetizer, showing that the detector worked well, and little else. So my colleague, professor Franco Simonetto, gave some thought at what meaningful physics measurement could be squeezed out of the few hundred thousand events collected by CMS before the winter shutdown, at 0.9 and 2.36 TeV of center-of-mass energy. And he came up with a brilliant find: Bose-Einstein correlations, of course!
Why You Always Liked Bose-Einstein Correlations But Were Blissfully Unaware
For a guy like me, who has always worked on high-Pt physics (a jargon naming of the processes which involve a large energy release in the collision of hadrons, eventually producing very massive bodies like the top quark, the Z boson, or the Higgs), id est frontier physics -using the colliding beams to reach as high as possible in available energy- switching to a kind of physics that involves studying the lowest-energy interactions looked nonsensical at first; and others in our group seemed perplexed. But it did not take us much to realize that the proposal made a lot of sense.
First, opportunity: the data was finally there -and it had been waited for more than a decade by some. The data allowed a meaningful measurement of Bose-Einstein correlations. Not much meaningful other than that could be extracted from the little speck of integrated luminosity.
Second, aggregation: by all dropping our pet analyses and concentrating on a single topic, we could finally create a strong group. Nobody would have a chance to lament having been diverted from his or her interest, because we all were!
And third, reward. As Franco pointed out, for some strange reason Bose-Einstein measurements in the past have all attracted dozens of citations in refereed physics journals. There seems to be a very active undergrowth of theoretical work on this topic. And rightly so: the physics of production of light hadrons is mysterious and fascinating. We cannot calculate it, and despite all the experimental measurements, there remain many puzzles still to be solved.
I have already had the occasion to discuss in short the phenomenon here. Bose-Einstein correlations in particle collision are a phenomenon that affects interactions producing two or more identical bosons. Bosons are particles possessing an integer value of the attribute called "spin" -think of it as the rotation of the particle around their polar axis if you need, although it does not make much sense from a quantum-mechanical standpoint. Now, there is a quantum-mechanical rule, first studied by Bose and Einstein, explaining that when the wave-functions of two identical particles of integer spin overlap in space, they amplify each other. Since particle wave-functions, when squared, describe the probability of finding the particle in a point of space with a given momentum, the net result is that the finding of a boson in a particular point of space increases the chance that a second identical boson occupies that same point.
I am going to be quite imprecise now, but it will be a minor sin. I am going to claim that by "identical" in the paragraph above you should read "having same attributes, including their momentum". This means that only identical particles that move with the same energy and direction produce the explained Bose-Einstein amplification. In more precise terms I should have explained that position and momentum should be treated more equanimously, but let us ignore this. I will anyway get back to this issue later on.
Because of the specification that only particles with the same momentum exhibit the phenomenon, we can actually study it at a particle collider! In fact, we would never be able to measure with the required precision the exact point of emission of a particle we reconstruct meters away in our detector; while we can measure particle momenta with more than adequate precision to select pairs which have equal momenta. This is enough to see whether we find more of those pairs than we predict.
The nature of the measurement might already dawn on you after the above explanation: you pick pairs of particles of the same charge, and count how many pairs you see as a function of how similar their momenta are. If you see an enhancement at very low "difference", that is due to pairs which were created together because of an increased probability -the Bose-Einstein effect!
You have to like the simplicity of this concept: by simply counting pairs of particles and cataloging their momentum difference, we get access to the secrets of their production mechanisms, and of the quantum mechanics of strong interactions in the crypt of the low-energy, non-perturbative regime which theorists have never accessed with direct calculations.
The CMS Measurement
If the above has not made you an enthusiast of Bose-Einstein correlation measurements yet, pry leave your share of this server's bandwidth to more meritorious minds. I am now going to explain some of the details of the measurement, which includes one or two appreciable finesses -the stuff that divides an excellent analysis from a mediocre one.
We start with about 300,000 0.9 TeV proton-proton collisions, and about 20,000 2.36 TeV collisions. These data were collected in a few days of running in December 2009. Helical tracks are reconstructed from the detected ionization left by charged particles in the dozen layers of silicon detector constituting the heart of the CMS detector (see picture, right): the radius of curvature of these tracks provides a precise measurement of the momentum of the particles, since the helices are produced by a precisely measured, uniform magnetic field; the curvature also determines whether the particle charge is positive or negative.
Most of the particles produced in the collisions are positive or negative pions: pions are the lightest hadrons, and proton-proton collisions have an easier time creating them in large numbers. We have ways to try and infer the identity of a track, but it is not necessary to apply them in our analysis. Rather, we "assume" ab imperium that all tracks are due to charged pions, and call "identical" two particles of equal charge. We thus proceed to pair up each particle with all the possible others of same charge in every event, to determine the Q-value of the pair, a variable which determines how similar their momenta are. Low Q-value means that the two particles have similar momenta, high Q-value means they are quite different.
Already between the lines a miracle has happened of no lesser entity than somebody else's fish and bread trick! We had an embarassingly small dataset -some hundred thousand events, corresponding to an integrated luminosity a few billion times smaller than the one currently available to the Tevatron experiments- and by considering particle pairs we are blessed by the spirit of Pythagoras, who multiplies the statistics. If the average event possesses N=12 tracks, 6 positive and 6 negative ones, we have 2xNx(N-1)/2=N^2-N=30 pairs to use for our measurement. Thus, by considering pairs rather than events, the 300,000 events become over ten million pairs. And even the meager 20,000 higher-energy bounty becomes a million-strong set of track pairs!
This is of course not our own concoction: all analyses of Bose-Einstein correlations in particle reactions enjoy the benefits of that miracle. However, it was wise of Franco to realize the potential of such analysis with our small data.
And what do we do with Q-values ? We may study it to see whether there is a enhancement at low values, of course. But a enhancement with respect to what ? What tells us if we see more pairs than we should ? We evidently need a reference sample of particle pairs for which there is no Bose-Einstein correlation, to compare Q-values.
Reference samples of pairs can be constructed in many ways. One simple choice is picking pairs of particles with opposite charge: the two particles in such pairs are for sure not identical, so they will not exhibit any Bose-Einstein correlation at low Q. But other choices are possible, which have some practical advantages. One such possibility is to pick a track in one event, and pair it up with a second track in the next event of the dataset: the two events know nothing of each other, so the two tracks will have by construction no possible correlation in their wave-functions.
In the end, we could put together seven different reference samples to which we compared the Q-value of our identical pairs. Each reference sample exhibits some very small differences from the signal sample, but they all have a very prominent feature: they have no signal at low Q-value. This is evident in the figure on the right below, where the ratio between the Q-value of signal sample and one of the reference samples is shown for data (black points) and Monte Carlo simulation (black histogram). The green line is at 1.0 and is just meant to guide the eye. The signal is prominent in the data, and both data and Monte Carlo have a slow dependence on Q-value across the board.
The small differences I mentioned above annoy us, since they require a detailed modeling to allow for a better measurement of the signal features present in the ratio. They can be washed away by using the simulated collisions of the Monte Carlo dataset. The simulation does not include a modeling of Bose-Einstein effects, and in fact in it we see no low-Q signal in the ratio between the Q-value of same-charge pairs and any of the reference samples one may construct. But the small differences are there, since they are due to the intrinsic features of our reference samples, which are generally well-simulated.
The above suggests that we construct a double ratio: by dividing the ratio found in the data (which shows a Bose-Einstein signal) by the ratio found in the simulation (which does not have any signal), we further "clean up" the distribution. What is left is a function almost perfectly lying at double ratio equal to 1, with a low-Q enhancement which is entirely due to the signal. Hail to double ratios!
Above you can see one of the seven double ratios we studied. These are clearly much better behaved, and can be modeled better by simple parametrization (the red curve, which is the sum of a flat line and an decreasing exponential).
In principle, we could be happy: we have seven ways to determine the parameters of the effect. But we want a better estimate. So we can "average" the seven reference samples into a "combined reference". This becomes mathematically more complicated, but there is nothing conceptually hard. The double ratio resulting from such exercise is shown below,
for 0.9-TeV data.
The crucial parameter in the fits is called r. This is basically a quantity measuring the size of the region within which, during the production of the pion pair, there was a constructive interference of the wave-functions. The fact that the size of this region -of the order of a fermi, or a millionth of a billionth of a meter- can be measured by comparing particle energies and directions is surprising, and yet is at the heart of the interference mechanism: position and momentum are conjugated variables, and as such information on one of the two is related to information on the other.
To make an improper parallel, we routinely determine decay times of particles down to the trillionth of the trillionth of the second, and smaller, by measuring the difference between the nominal mass of the particles and the energy released in the decay -the so-called "width of the resonance". Again, it is the conjugation of energy and time in the quantum-mechanical formulation of the particle wave-function coming out quite handy.
Our data allows us to measure the r parameter in both 0.9-TeV and 2.36-TeV datasets. While at 0.9-TeV r had been determined in the past, ours is the first measurement at the higher energy point. And so we find something interesting: r is found to grow significantly with energy.
The two results are in fact r(0.9 TeV) = 1.59 +- 0.05 +- 0.19 fm, r(2.36 TeV) = 1.99 +- 0.18 +- 0.24 fm. These are different by about two standard deviations (systematic uncertainties are 100% correlated). Not a definitive proof yet, but a strong indication, considering that the increase was expected by theoretical models.
Another interesting thing that we found was a dependence of r from the number of particles produced in the collision: a very clear trend is observed when, before performing our r measurements, we divide our data in subsamples of events having similar particle multiplicities. Check it out in the graph below, which shows how r more than doubles when one goes from low- to high-multiplicity events.
The above effect is not new: other experiments had observed a trend in r with particle density (a differential of the particle multiplicity by angle of emission). However, this is in my opinion a significant addition to the knowledge of Bose-Einstein correlations.
Concluding remarks
I think I can summarize in two lines this abnormally-long article.
Line one: CMS has starting to produce brand new physics results, in an energy regime never so far investigated.
Line two: the group of CMS physicists in Padova we have created rocks!
Nine of us have authored this study: my collegues are Paolo, Mario, Stefano, Martino, Massimo, Luca, Franco, and Ezio. And it is with them that tomorrow afternoon, during the monthly meeting of CMS-Padova, I will uncork a fine bottle to celebrate! There is indeed something to celebrate: not just the publication (and the future Physical Review Letters article) that we produced, but the successful collaboration we have put together. In the last three months we have been in a sort of permanent meeting -day and night, five in a room working elbow by elbow or each of us scattered around three countries talking through skype or Evo, with thousands of e-mails exchanged among us, with our reviewers (which I duly thank for the responsiveness and help: Pierre, Vitaliano, and Monica).
And, lest I forget: this article would not be publishable if I omitted to include a link to the official CMS documentation. It's the rules of the game now! The public document can be find at this link.
And now for something different... We have already jumped on the 7-TeV collisions currently pouring into our hard disks, to produce the first analyses with muons. Stay tuned!
