Elementary calculations show that the mass of the passenger's vehicle should have an important influence on risk of injury, greater mass yielding greater protection independent of the other mass(es) in the collision. This holds for collisions treated either as purely elastic, or as quasi-inelastic. Passengers in more massive vehicles thus would seem better off no matter what the size or weight of other vehicle(s) in a collision.

The approximations used suggest that highway vehicles should be at least 20 times the mass of the average passenger, or injuries in a collision will be disproportionately grave.

Introduction

Ross and Wezel [1] state that the role of mass and crush space on passenger injury in an automobile collision are not understood. However, a related and vital concern for the safety of the passenger can be approximated in an enlightening way: We shall show that, for automobiles, the less massive the vehicle occupied by a passenger, the greater the momentum transferred, and so the greater the risk of injury, other things being equal. This argues for mass as a safety factor independent of considerations of the relative masses of two colliding vehicles.

Problem Analysis

The problem can be solved in the most general terms only by elementary methods.

Consider three masses, M_X, M, and m, lined up left to right in that order, with M and m slightly separated and at rest with respect to one another.

We shall let M and m represent the passenger's vehicle and the passenger, respectively (see Fig. 1).

Let the other vehicle, of mass M_X, approach the passenger's vehicle at the collision velocity V_X.

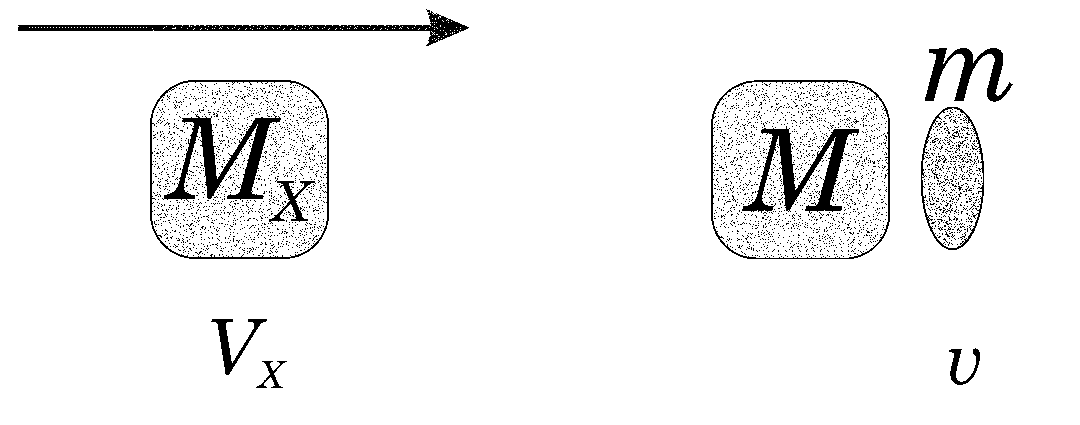
Figure 1.

We wish to know the velocity v imparted to the passenger of mass m in the rest frame of M; it is the impulse to this velocity which will cause all injury directly caused by the collision.

We are concerned only with the change in velocity of the passenger, which change will represent momentum transferred to the passenger by the passenger's vehicle; the new velocity v of the passenger will be relative to the passenger's vehicle. So, our calculations will hold regardless of whether the MX or M vehicles, or both, began in motion relative to the road. Of course, ejection of the passenger would have other effects -- all more serious than those calculated here -- depending on the speeds of the vehicles on the road.

We first approximate the mechanics by assuming an elastic collision in which momentum is distributed among the vehicles and the passenger, but in which no energy is lost during the collision. We then modify the analysis to account for energy absorbed by the vehicles; we call the result a quasi-inelastic analysis, because it represents an inelastic collision with energy losses represented only as totals for each vehicle. Finally, we propose a correction to the quasi-inelastic analysis for the special case in which the passenger's vehicle is very light, approaching zero mass; this correction is approximately rigorous and allows the quasi-inelastic analysis to be applied for insight into cycling or even pedestrian collisions.

Elastic Analysis.

The one-dimensional formula for final speed of an elastic body colliding with another is easily derived from conservation laws and may be found in elementary physics texts. We first derive this general formula, because it is useful and can be applied to other general problems as well as to object-by-object detailed simulations. Then, we apply the general formula to our collision problem.

Assume an object of mass m₁ initially in motion and another of m₂ at rest; after a collision, we seek the final velocity of m₂. Let subscripts i and f refer to initial (before collision) and final (after collision) states, respectively. Then, we may define the total initial momentum as p_i = m₁v_1i. Using conservation of momentum, after collision the final momentum p_f will be equal to the initial and will be distributed between both masses so that p_i = p_f = m₁v_1f + m₂v. We seek v (same as v_2f) and immediately may write

Equation (1):

We are not interested in the impulse on m₁, so we want to eliminate v_1f in Eq. (1); we use conservation of energy for this: The initial kinetic energy will be, m₁v_1i²/2. The final energy will be equal to the initial and will be distributed between both masses; so, m₁v_1i² = m₁v_1f² + m₂v²; and, thus, v_1f² = (m₁v_1i² - m₂v²)/m₁. If any energy were lost, the collision would not be elastic. Substituting into (1), we get m₂v = m₁v_1i - m₁[(m₁v_1i² - m₂v²)/m₁]^1/2; which reduces to,

Equation (2):

so,

Equation (3):

This general formula gives the velocity v added to a second body of mass m₂ after collision at relative velocity v₁ with the first body of mass m₁.

Applying the formula of Eq. (3) twice in our collision problem in left-to-right order, once for impulse on the passenger's vehicle of mass M, and again for impulse on the passenger of mass m, the result is a simple product and may be written,

Equation (4):

In an idealized automobile collision, the mass of the oncoming colliding vehicle may be taken as, say, somewhere between 10m and 30m. This means that, for a 75 kg (165 lb) passenger, the oncoming vehicle would weigh between 750 kg and 2250 kg--in the passenger car to light truck (or SUV) range.

For generality and convenience of units setting V_X = 1 and m = 1, Eq. (4) is plotted in Fig. 2 as a function of the mass M of the passenger's vehicle.

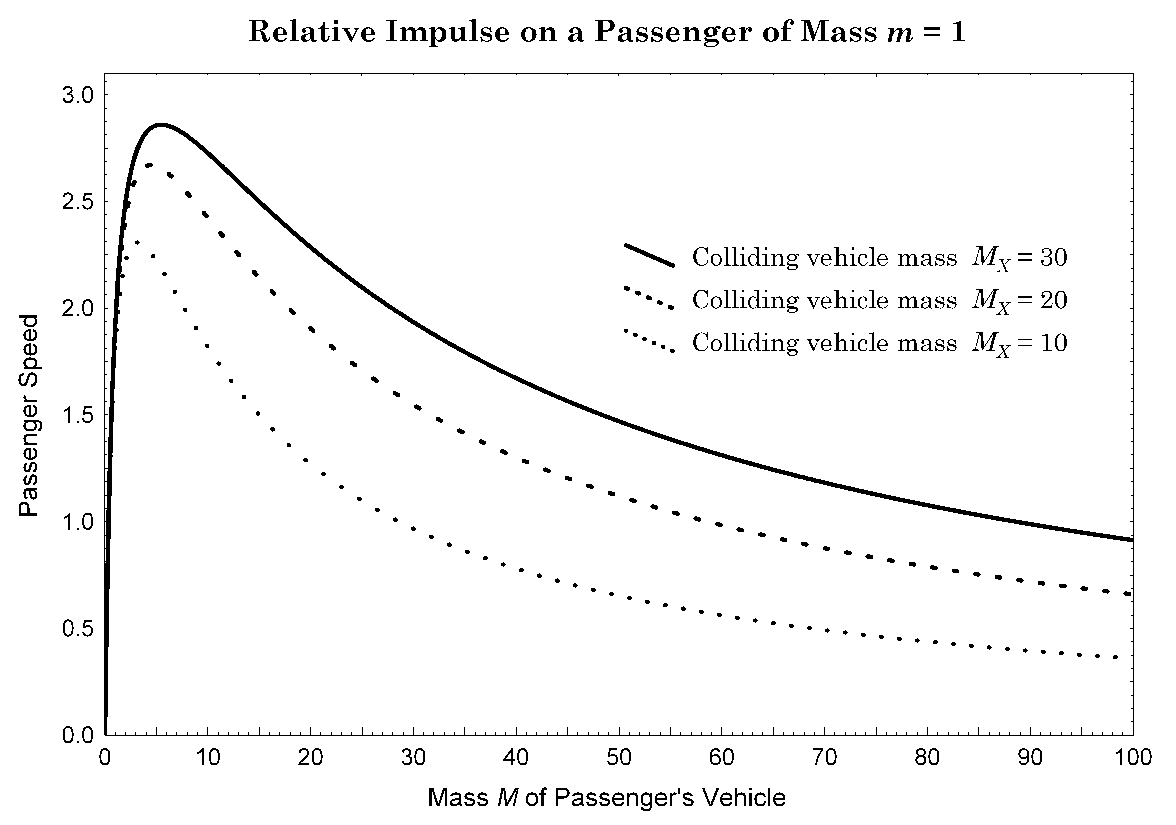
Figure 2. Speed imparted elastically to a passenger in a vehicle of mass M, struck by a vehicle of mass M_X moving at relative speed V_X = 1. Uncorrected for M 10 or so.

It might seem from Fig. 2 that the severity of injury to the passenger should peak for a vehicle around three to six times the mass of the passenger; however, the initial, rising phase of the curves may be considered an artifact, because, with M extremely small, a collision of vehicles of masses M_X and M + m really should be treated more as a direct collision of objects of mass M_X and m. A correction to the curves for M near zero will be made below.

Note that this analysis does not depend on the orientation of the colliding vehicles (side versus head-on) or the location of the passenger. It is a completely general center-of-mass result. Orientation and location factors may be accounted for in the relative energy absorption factors of the quasi-inelastic analysis to be considered next.

Quasi-Inelastic Analysis.

It is easy to adapt the above approach to account for the energy loss because of inelastic collision. However, as Ross and Wezel [1] point out, the prolongation of total impulse because of spatial factors, and the conditions of crushing injury, are not well understood or easily described. These are specific to a particular collision, not general, and we shall not address them here.

We may assume that a certain fraction of the kinetic energy will be lost in the M_X to M vehicle-to-vehicle contact; call this fraction deltaE_MM. This mainly would be because of deformation, deflection, or ejection of parts of the two vehicles. Likewise, because of dash padding, air bag inflation, and similar factors, a fraction, deltaE_Mm, of the remaining kinetic energy will not be transferred from the passenger's vehicle of mass M to the passenger of mass m. Kinetic energy is proportional to v², so we may account for inelastic losses simply by scaling each value of changed speed v_j by sqrt(E_j).

We therefore may write down the quasi-inelastic modification of Eq. (4) as,

Equation 5:

As a rough estimate, let us assume that half of the vehicle-vehicle collision energy was lost and thus became unavailable to injure the passenger; then, deltaE_MM = 1/2. Likewise, let us assume that the safety apparatus or good fortune of the passenger's vehicle makes deltaE_Mm = 3/4. Using Eq. 5, the result is shown in Fig. 3, for the same other conditions as in Fig. 2.

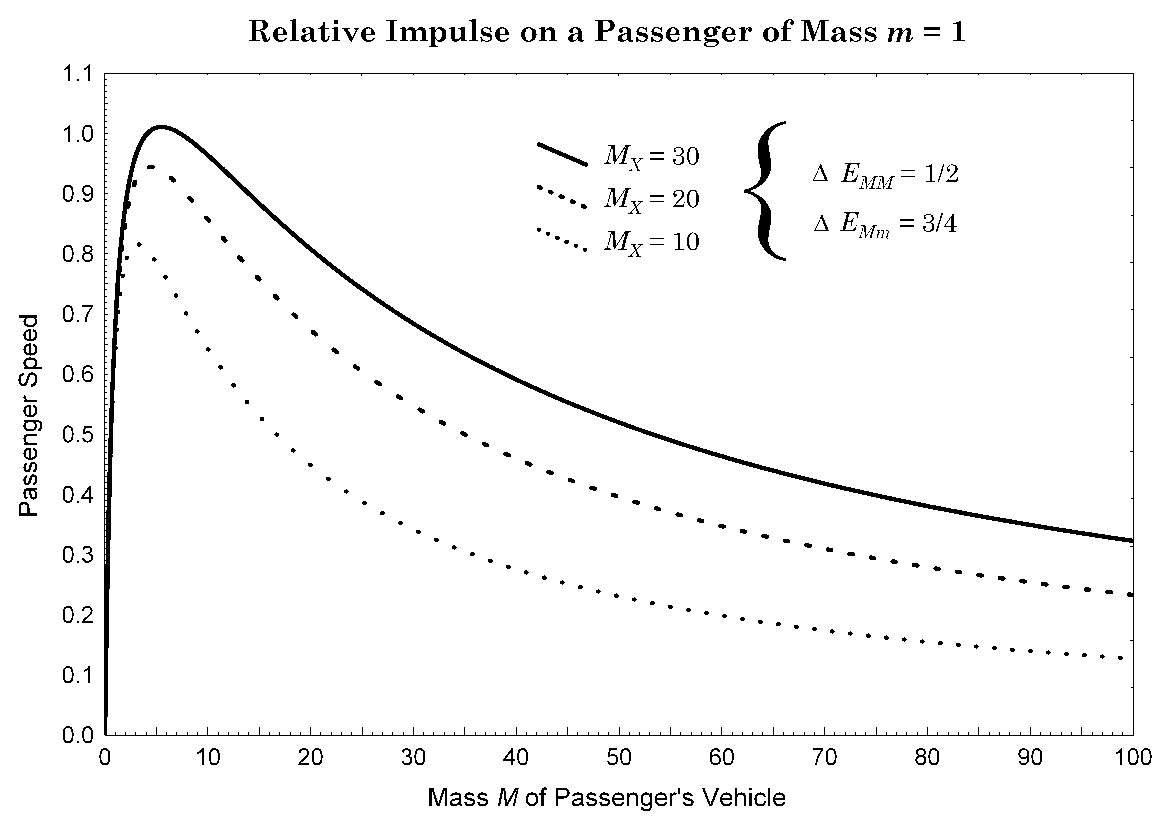
Figure 3. Quasi-inelastic speed imparted according to text Eq. (5) to a passenger in a vehicle of mass M, struck by a second vehicle of mass M_X moving at speed V_X = 1. Uncorrected for M 10 or so.

The curves in Fig. 3 have the same shape as those in Fig. 2, the lost energy only causing a scaling down of the whole curve. The peaks near M = 0 remain uncorrected; but, no matter how much energy is absorbed by the vehicles or otherwise diverted to protect the passenger, the shapes of the curves do not change between the elastic and quasi-inelastic cases: Only the relative heights change as a function of the fraction of energy lost. Therefore, the present analysis, at least away from M = 0, will be valid regardless of the actual energy loss during a collision. The uppermost peak value in Fig. 3 is near 1.0 by coincidence.

The advantage of a very massive vehicle, such as a multiaxle truck, bus, or train, is obvious in Fig. 3. Using the peaks of the curves in Fig. 3 as the worst case, even when the colliding vehicle is very light compared to the passenger (curve M_X = 10), a mass M of at least 25 times the mass of the passenger would be required to reduce by 1/2 the impulse to the passenger. The farther out to the right the passenger vehicle's mass, the less the potential injury to the passenger.

Notice that even with about 7/8 of the energy absorbed by the vehicles, a passenger in a light vehicle can be accelerated to a speed equal to that of the collision itself (curve M_X = 30, peak).

Considering the point of greatest upward curvature of the curves in Fig. 3, the result implies that a vehicle weighing less than about M = 20 times that of an average passenger, or 1,500 kg (1.7 English tons), puts the passenger at an inherent disadvantage in a collision, regardless of the nature of other vehicles involved. Lighter vehicles disproportionately increase the risk of injury; heavier vehicles more gradually mitigate this risk.

It is notable in Fig. 2 that the elastic-model speed imparted by impulse to the passenger always exceeds that of the collision itself, unless the passenger's vehicle is at least three times the mass of the colliding vehicle. Energy absorption by the vehicles is an extremely important safety factor, as confirmed by the present analysis.

Also interesting is that when two vehicles are exactly of the same mass, the risk of injury seems to be almost independent of vehicle mass. This is not a realistic interpretation, though, because two colliding vehicles never will be exactly equal in mass, even when they are manufactured to the same weight and have all the same manufacturer options: The cargo, if any, will differ, the gas in the tanks will differ, and the number and weight of the seat-belted passengers will differ. Because the slopes of all curves in Fig. 3 increase with decreasing mass (M or M_X), lighter vehicles amplify vehicle weight differences more than do heavier vehicles. Thus, there is a reduced risk of injury in collision of two relatively massive vehicles, for all passengers, even when the vehicles are only slightly different in mass.

Correction for Very Light Vehicles.

The calculations shown in Figs. 2 and 3 assumed always two vehicle masses and one passenger mass. For very light passenger vehicles, the impulse curve approached zero for values of M near zero, implying that perhaps extremely light vehicles such as bicycles, motor scooters, or motorcycles somehow might be safer than more massive ones. This is an artifact of the assumption that the passenger's vehicle absorbs energy and transfers all momentum received by the passenger, an assumption which clearly is false when the passenger is exposed more and more to direct contact with the colliding vehicle.

So, the curves in Fig. 3 can not be correct at values of M close to 0. To correct these curves at very low values of M, we shall assume no passenger vehicle, estimate the quasi-inelastic impulse on a passenger of unit mass, and then patch the result in to the high-mass curves in Fig. 3.

With no passenger vehicle, the total initial momentum again is p_i = m₁v_1i. The derivation was done already above, so Eq. (3) is replaced by,

Equation 6:

The small passenger vehicle, of vanishing mass not shown in Eq. 6, still may be assumed to absorb some energy deltaE_MM in contacting the colliding vehicle. The quasi-inelastic formula for an exposed passenger on a very light vehicle then may be written,

Equation 7:

Eq. (7) is plotted in Fig. 4 as a function of colliding vehicle mass for several values of deltaE_MM. Notice that the passenger's impulsive speed approaches 2 (twice the speed of the collision) for the elastic case deltaE_MM = 0 as the mass M_X of the colliding vehicle increases.

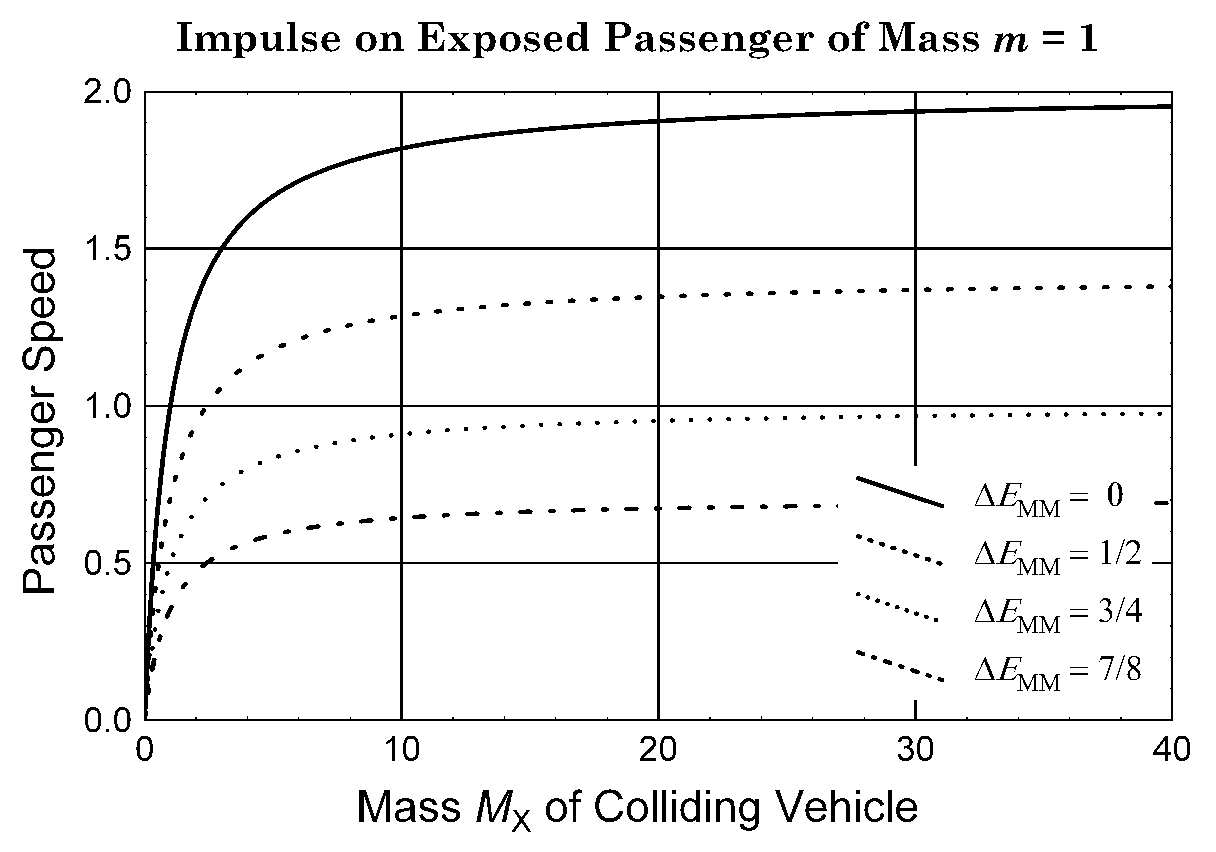
Figure 4. Quasi-inelastic relative impulse at unit speed on a passenger in a vehicle of negligible mass. Text Eq. 7 as a function of colliding-vehicle mass.

Comparing Fig. 2 with Fig. 4, it might seem strange that, in an elastic collision with a vehicle of mass 30m, a passenger in a vehicle of mass 25m could be transferred the same impulse speed (v = 2) as a passenger on a bicycle or other negligibly light vehicle. This is a peculiarity of the elastic model of transfer of momentum.

The results in both figures are correct, as may be understood by a simple analogy: Imagine two identical, hard, perfectly elastic steel balls which can roll in a horizontal trough so they collide always dead center. Leave one at rest in the trough and roll the other one into it: the first one will stop while the second one carries off all the momentum. If something is to be hit by a ball at the end of the trough, it doesn't matter whether just one ball was rolled or the first ball was rolled into the other: The ball arriving at the end will have the same momentum.

Similarly for the Fig. 2 elastic collision model presented here: In the elastic case, the colliding vehicle transfers all its momentum to the passenger's if M equals M_X; it still transfers a substantial fraction of it if M is somewhat different from M_X. Thus, in an elastic collision, where nothing absorbs any energy, the passenger might as well be hit by the colliding vehicle directly, if the passenger vehicle has about the same mass as the colliding one. Of course, real collisions never are perfectly elastic, at least ones which cause damage.

What is important in Fig. 2 or 3 is that, when examining the relative effect of the mass of the passenger's vehicle, a comparison which can not be done in Fig. 4, the mass of the passenger's vehicle visibly has a protective effect whenever the mass is substantially greater than that of the passenger.

Now, let us proceed to the correction of Eq. (5) by means of Eq. (7):

It's easy to bound the correction: First, the impulse at M = 0 in Fig. 3 can not possibly exceed 2, because 2 would imply a perfectly elastic collision by an infinitely massive colliding vehicle, with all possible energy delivered to the passenger.

Second, consider that in a quasi-inelastic collision, other things being equal, if passenger vehicle mass M decreased nearly to 0, the absorbed fractions of the kinetic energy, deltaE_MM and deltaE_Mm, would be expected to decrease also. So, using the values of absorbed energy assumed in Fig. 3, we know that the correction must make the curves intersect the M = 0 ordinate somewhere above the value in Fig. 4 corresponding to deltaE_MM = 7/8; this means above about v = 0.7.

Therefore, the correction to Eq. (5) must make all curves intersect M = 0 somewhere between v = 0.7 and v = 2.

The only remaining question in the correction is that of how the decreasing absorbed energy should affect the impulse as the passenger vehicle's mass approaches M = 0. The result at M = 0 again is described by Eq. (7), which is replotted as a function of absorbed energy in Fig. 5.

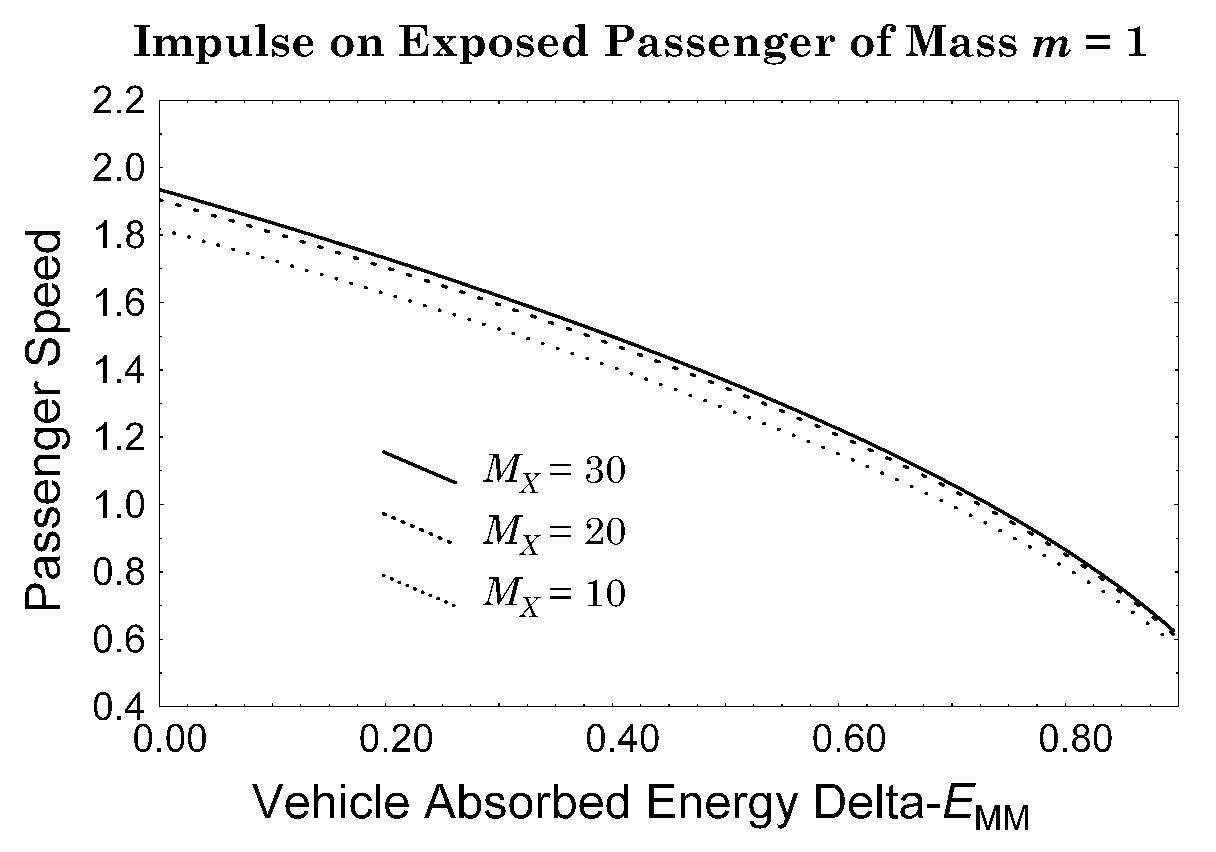
Figure 5. Quasi-inelastic relative impulse at unit speed on a passenger in a vehicle of negligible mass. Text Eq. 7 as a function of absorbed energy.

As obvious in Fig 5, the three curves of Fig. 3 must be corrected to intersect the M = 0 axis within about 0.1 of one another.

There is a certain arbitrariness in any correction of the present analysis for very light vehicles, because the two relevant equations, Eq. (5) and Eq. (7), differ fundamentally in that Eq. (7) can include only one energy absorption term. deltaE_Mm is set to 0 in Eq. (7), but an equally valid way of representing a very light passenger vehicle would be to set deltaE_MM to 0, or to reduce both of them toward 0 together. Actually, there is some arbitrariness in the problem itself, however represented, because the same collision masses may be obtained by a variety of different vehicles; and, imagining the same passenger in a sequence of less and less massive vehicles, down to a mass of 0, necessarily involves discontinuities and an arbitrary variety of possible alternatives.

We choose to resolve this arbitrariness by assuming that Eq. (5) is exactly correct for passenger vehicle masses of 15m or more, and that Eq. (7) gradually becomes the better representation as the mass below 15m approaches 0. The result is not very sensitive to the exact value, 15m, but patching the curves together at a cut lower than 15m makes a slight jog in the slope more noticeable than otherwise.

For our correction, we set deltaE_MM in Eq. (7) to the total effect of deltaE_MM and deltaE_Mm in Fig. 3 at M = 15m, and then we let deltaE_MM approach zero proportionally to M. In combination with letting deltaE_MM go to zero this way, in the range between M = 0 and M = 15m, we sum the contributions from Eq. (5) and Eq. (7) weighted linearly from 0 to 1 for Eq. (5) and from 1 to 0 for Eq. (7). The result is given by Eq. (8), in which V_X = 1, m = 1 and the high-M deltaE = 7/8:

Equation 8a:

Equation 8b:

Equation 8:

Thus, the total vehicular absorbed energy can be made to decline to 0 as M does, as one might wish, and the influence of the Eq. (5) result, which includes two vehicle masses, also becomes negligible as M goes to 0. This is an advantage of the way we have defined a quasi-inelastic collision.

For comparison with Fig. 3, the Eq. 8 correction is shown in Fig. 6.

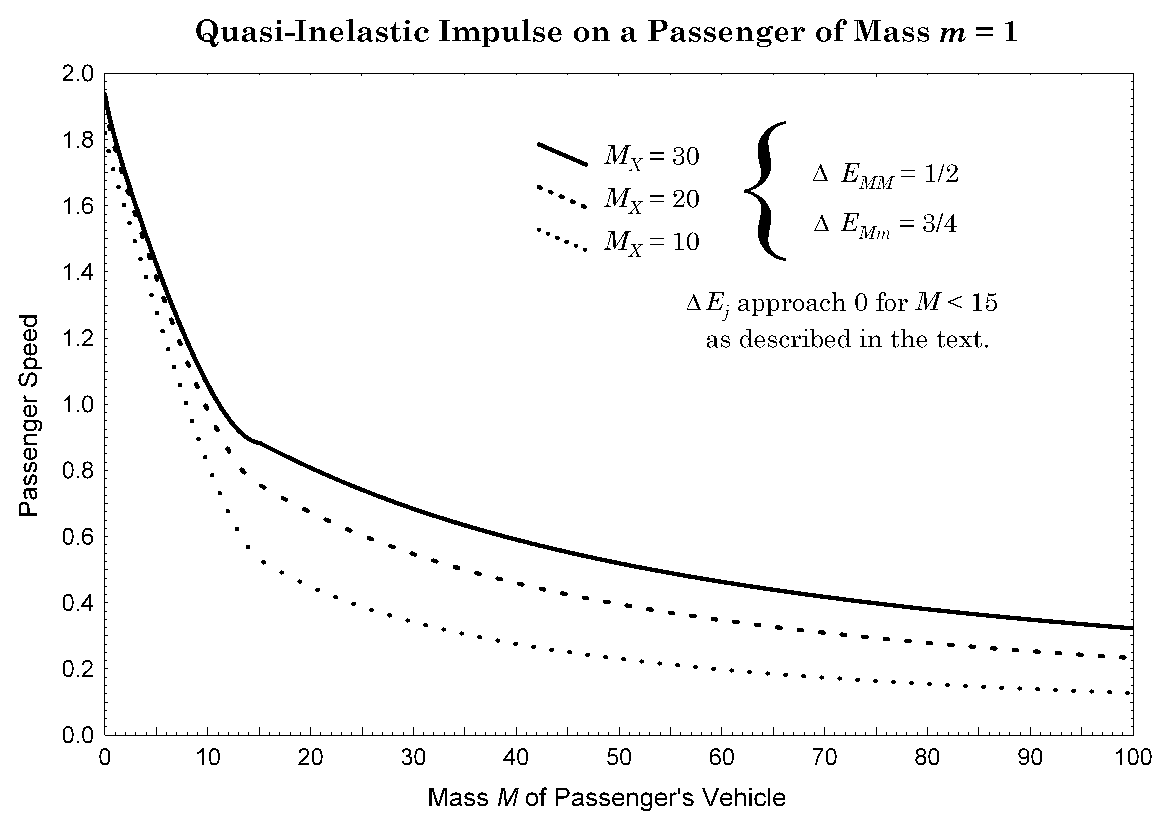
Figure 6. Quasi-inelastic-model speed imparted to a passenger in a vehicle of mass M, corrected for small M as in Eq. (8). Compare with Fig. 3.

Generalizing the correction of Eq. (8), Fig. 7 shows the final result for impulse transferred to the passenger as a function both of mass M of the passenger vehicle and mass M_X of the colliding vehicle.

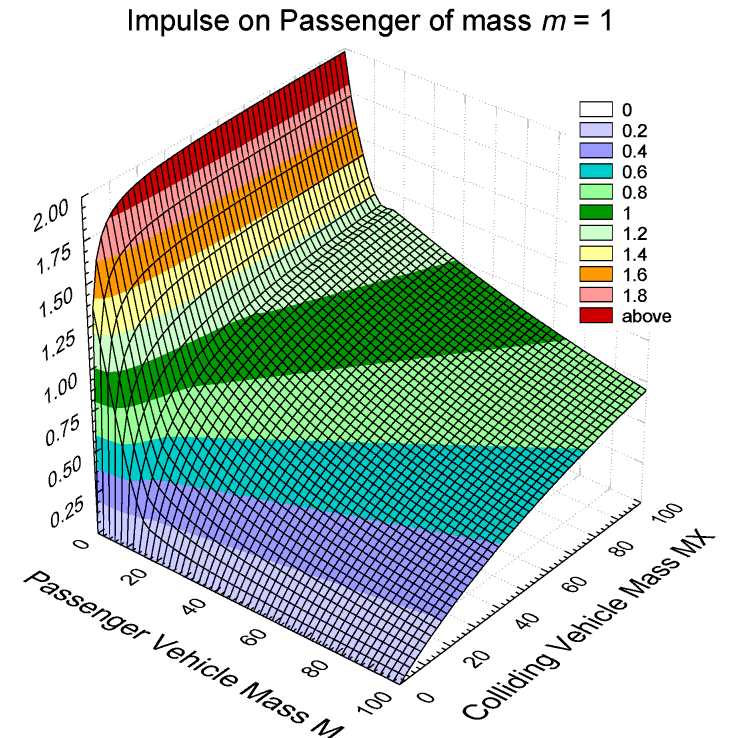
Figure 7. Impulsive speed delivered to a passenger as a function of vehicle mass. Collision speed V_X = 1. Total energy loss deltaE = 7/8 when M>15m. Quasi-inelastic generalization of Eq. (8) corrected at low M as described in the text.

Conclusion

We have attempted to clarify the effect of the mass of a vehicle on the impulse transferred to a passenger in that vehicle during purely elastic or quasi-inelastic collisions.

The result indicates that there always is extra risk of impulsive injury in riding in a relatively light vehicle, no matter what the safety appliances installed, and regardless of the weight of the other vehicle or object(s) involved in a collision.

This conclusion, even to the steep slope at low passenger vehicle mass M, is borne out by data [2] recently released by the U. S. Department of Transportation, National Highway Traffic Safety Administration, and based on vehicle weight statistics for crashes during the period 1995 through 2000. The result also is consistent with the completely empirical quantification of the problem by Evans [3].

References

1. Ross M, Wezel T, Losing Weight to Save Lives: A Review of the Role of Automobile Weight and Size in Traffic Fatalities, Physics and Society, 31(1), 9 - 12 (2002).
2. Kahane C J, Vehicle Weight, Fatality Risk and Crash Compatibility of Model Year 1991-99 Passenger Cars and Light Trucks, NHTSA Technical Report DOT HS 809 662 (October 2003), http://www.nhtsa.dot.gov/cars/rules/regrev/evaluate/pdf/809662.pdf.
3. Evans L. Causal influence of car mass and size on driver fatality risk. American Journal of Public Health, 91, 1076 - 1081 (July 2001).