Taylor's Theorem is Everywhere.

At about the 1 minute mark in a youtube Yale Lecture, titled The Taylor Series and Other Mathematical Concepts, the teacher tells his class that he will be presenting the Taylor Series and the class erupts into laughter. Why? As an undergraduate, I vaguely recall my dissatisfaction with Taylor's Theorem. It says that, for a well behaved function f(x),

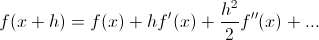
[It takes other forms depending on conventions. For example, the few sites I've checked set x=0 and let h be the parameter and call it x.
B.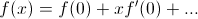
There is also a Remainder Term that involves an integral that, following Taylor's original paper, I've neglected to include.]

In words, this says that, given f(x) and a small parameter h, we can evaluate f(x+h) by merely evaluating f(x). If we know f(x), we know f(x+h) to an arbitrarily high accuracy. In physics, the h squared term and higher are often neglected.

So why did this bother me? I believe I thought something like "if I have a function, why not simply evaluate it at f(x+h) if that is what I want to know?" My guess is that is partly the reason for the eruption of laughter in the classroom.

Here some responses to that:

1.You don't always have a function. Sometimes all you simply assume that there is a well behaved function and you use that fact and Taylor's Theorem to find a result. For example, in D'Invernio's excellent GR textbook, Introducing Einstein's Relativity, we find the following argument:

2.Even if you have an explicit function, it is sometimes easier to calculate the function for a particular value (or the function might simply be known for that value) and use the Taylor series to extrapolate to the f(x+h) value. For the ordinary function cos(x) it is tricky to calculate cos(.07) without using the fact that cos(.07)=cos(0)+[.07^2] /2 cos(0)+...

3. The Taylor Series might be more informative than the explicit function.
Using the Taylor Series for functions like e^x, sinh(x), cosh(x), sin(x) and cos(x) makes it very simple to prove most trig identities, facts about the derivatives of these functions, and the famous relation

For example, in the Yale lecture, the uses the Taylor's series, in form B above, to calculate

Applying this to Einstein's expression for the relativistic energy of an object moving with velocity v gives

and the professor, with a wave of his hand, remarks that for 300 years we did mechanics keeping just the second term.

[And, out of curiosity, I've opened my copy of The Principles of Relativity to Einstein's original paper, Does The Inertia of a Body Depend Upon its Energy Content?, and found him stating that

"Neglecting magnitudes of fourth and higher order." Something that has always amazed me about Einstein's papers is that his arguments are largely the ones still used today. His 1916 paper on General Relativity could serve as an outline for any modern introductory GR course and could also serve as an introduction to the subject with provided it is supplemented with a textbook like Introduction to Vector and Tensor Analysis by Robert Wrede. The last chapter of Wrede is the most succinct account of the fundamentals of GR I have found and I recommend it to anyone interested in GR with some knowledge of vector calculus.]

4. The Taylor series