What I didn't account for in my last blog post was that there is a first order energy shift due to classical physics.. to IS NOT relativitstic in nature.
This can be understood using E=hf and the classical doopler shift which has v/c as a first appoximation and v^2/c^2 as a second approximation.
The relativitc approx (1-v/c) (1+v/c +v^2/c^2) - (1+v/c)(1+v/c+v^2/c^2) gives 1+v^2/c^2. The first order effect cancels leaving only the second order purely relatvistic effect.
Without relativity
If the rays are pointed in the same direction this cancellation of first order effects doesn't occur.
Is it possible to understand this without reference to the doopler effect? Is there some reason ...
push the analogy:
transverse doopler - beams going in opposite
classical -beams going in the same direction
In Einstein's original derivation of E=mc^2, he choose his light signals moving in opposite directions. I thought this was merely to make the mathematics simpler, but if the experiment was done with only one beam moving to the right with energy L, the derivation would not work. Because in that case, the approximation in kinetic energy shift would be given by the much larger 1+v/c instead of 1+v^2/c^2. There is nothing, as far as I can tell, in his original paper to justify taking the beams in opposing directions.
Somehow the symmetry prevents the .....
It wasn't exactly known at the time but the energy shift due to relativity and the energy shift due to nonrelativistic effects can be determined... using planks formula...
Now back to Einstein's original derivation:
By having the beams move in opposite directions he has captured the mathematics of the transverse doopler effect. Having the beams move in opposite directions appearantly cancels out the first order effects due to the standard doopler effect and leaves the relativstic effect.
Why?
The cheap answer: 1. Because it reproduces the math of the transverse doopler effect
2. Because the classical amount of the energy of light doesn't depend on velocity. In pre-relativity the amount of energy of 2 light rays moving in the same direction is the same as two light rays moving in opposite directions. So by having his beams go in opposite directions he cancelled out the first order effect and left the second order effect...
So lets do it again with the radial, only this time taking higher order terms....
In my last blog, I guided the reader through Einstein's derivation of E=mc^2. The derivation involved a relativistic transformation equation for the energy of light. When I later came across the formula E=hf, it occurred to me that I should be able to employ the exact same argument, but instead of using the small velocity approximation to the relativistic equation for tranformation of energy of light, I would use small velocity approximation of the relativistic frequency shift. The small velocity approximation of the relativistic doopler effect is the classical doopler formula.
The new experiment is performed once with box moving and then again with box stationary. Like the original experiment, the only difference between the two experiments to two experiments is the kinetic energy of the box. So, unless I'm mistaken, similar reasoning applies and
In order to stress the analogy with the experiment in the previos post, the orginal energy, L=hf and the shifted energy is L=h(1+v/c)
Call E_0 the energy of the box prior to emission as detected by a stationary receiver
and call H_0 the energy of the box after emission, as detected by the moving observer.
Then E_0 = E1+hf
and
H_0 =H_1+ h(1+v/c)
(E_0)-(H_0) - (E_1)-H_1)
Again, the only difference between the two E-H terms is the kinetic energy of the box, but now, given L=hf, K_0 - K_1 = L(v/c).
There is no v^2 or 1/2 term so the calculation has given the incorrect result?
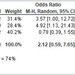
Oddly, this calculation gives the correct result is the receiver is moving transverse to the detector! (See the formula for the transverse Doopler Effect)
My thoughts. I think it is interesting that the transverse doopler effect gives the correct result, because the transverse effect is purely relativistic. There is no classical transverse doopler effect.
K_0-K_1= h(v/c)f=v/c L
If the relativistic doopler shift was approximated by (1+v^2/c^2) the result would have been correct
Assuming that the source (the box in our case) is moving toward the receiver
SEE THE PRINCIPLE OF RELATIVITY PAGE 56!!!!!!!!!!!!!