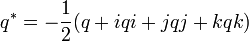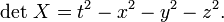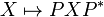Because Quaternions are things that act according to a general algebraic mathematical structure, they manifest themselves in a variety of ways in physics. The structure of Quaternion algebra is common knowledge and I refer the reader to wikipedia for the details. For the readers convenience, I'll quote what I consider to be the essentials here. Then I will ask questions that I will attempt to answer in the next blog. I would like my readers to answer or provide suggestions in the comment section too. This blog will contain nothing original other than the questions I ask. I am new to group theory and quaternions. Do not assume my questions are well posed. If you are familiar with Quaternions and Group Theory, then skip the quotations and read the questions.
Quaternions (Real Valued)
A. The Algebra
As a set, the quaternions H are equal to R4, a four-dimensional vector space over the real numbers. H has three operations: addition, scalar multiplication, and quaternion multiplication. The sum of two elements of H is defined to be their sum as elements of R4. Similarly the product of an element of H by a real number is defined to be the same as the product in R4. To define the product of two elements in H requires a choice of basis for R4. The elements of this basis are customarily denoted as 1, i, j, and k. Every element of H can be uniquely written as a linear combination of these basis elements, that is, as a1 + bi + cj + dk, where a, b, c, and d are real numbers. The basis element 1 will be the identity element of H, meaning that multiplication by 1 does nothing, and for this reason, elements of H are usually written a + bi + cj + dk, suppressing the basis element 1. Given this basis, associative quaternion multiplication is defined by first defining the products of basis elements and then defining all other products using the distributive law. -Wikipedia. Quaternions
The algebra of the basis elements 1,i,j,k is defined by
B. Other Properties
Conjugation of quaternions is analogous to conjugation of complex numbers and to transposition (also known as reversal) of elements of Clifford algebras. To define it, let q = a +bi +cj + dk be a quaternion, then the conjugate q*=a-bi-cj-dk... Conjugation is an involution, meaning that it is its own inverse, so conjugating an element twice returns the original element. The conjugate of a product of two quaternions is the product of the conjugates in the reverse order. That is, if p and q are quaternions, then (pq)* = q*p*, not p*q*.Unlike the situation in the complex plane, the conjugation of a quaternion can be expressed entirely with multiplication and addition:
Conjugation can be used to extract the scalar and vector parts of a quaternion. The scalar part of p is (p + p*)/2, and the vector part of p is (p − p*)/2.The square root of the product of a quaternion with its conjugate is called its norm and is denoted ||q||. (Hamilton called this quantity the tensor of q, but this conflicts with modern usage. See tensor.) It has the formulaUsing conjugation and the norm makes it possible to define the reciprocal of a quaternion. The product of a quaternion with its reciprocal should equal 1, and the considerations above imply that the product of and (in either order) is 1. So the reciprocal of q is defined to be
Wikipedia. Quaternions.
Question 1: The Lorentz Group is the set of elements that preserve the Minkowski Metric. Can we define Quaternions as the set of elements that preserve the Quaternion Metric? If yes,
Question 2: Is there a notion of conjugation of a Lorentz Vector? Can such a notion be developed in "Complex Lorentz Space"?
Also,
*A distance can be defined in terms of the norm, thus making Quaternions into a Metric Vector Space.
There are several useful representations of Quaternions including:Using 2×2 complex matrices, the quaternion a + bi + cj + dk can be represented as:
Wikipedia. Quaternions.
The real linear span of the Pauli Matrices and the 2X2 Identity Matrix is isomorphic to the real algebra of quaternions...As the quaternions of unit norm is group-isomorphic to SU(2), this gives yet another way of describing SU(2) via the Pauli matrices. Wikipedia.Pauli Matrices
The Lorentz Group and its representations:
As mentioned above, the Lorentz Group is the set of elements that preserve the Minkowski Metric:

The Minkowski Norm:

The Minkowski inner product (Norm) is a map η: M × M → R (i.e. given any two vectors v, w in M we define η(v,w) as a real number) which satisfies properties (1), (2), (3), (4) ...(sic)... 1.bilinear η(au+v, w) = aη(u,w) + η(v,w)for all a ∈ R and u, v, w in M. 2. symmetric η(v,w) = η(w,v) for all v, w ∈ M. 3.nondegenerate if η(v,w) = 0 for all w ∈ M then v = 0. 4.The bilinear form η has signature (−,+,+,+) or (+,−,−,−). Wikipedia. Minkowski Space
Question 3: Quaternions have a dual role. They represent group actions, but they can also represent components of a physical field. In relativity, 4-Vectors and Lorentz Transformations have different roles. 4-Vectors don't act on 4-Vectors and Lorentz Transformations aren't constructed out of 4-Vectors (not by multiplying them at least). How can Quaternions represent 4-Vectors and Lorentz Transformations? Is this aspect of Quaternion representations useful? How?
Question 4: The Minkowki Norm is 1.bilinear, 2.symmetric, 3.nondegenerate and has signature 4. What corresponding properties does the Quaternion Norm (or, perhaps, the Quaternion Metric) Satisfy? If it doesn't satisfy these properties, what difficulties does this imply for relating Quaternions to Lorentz Transformations.
Question 5: Given that the Real Quaternion Group and the Lorentz Group have different signatures, and signatures are preserved by similarity transforms that also produce equivalent matrix representations, can a truly equivalent 4D Quaternion representation of the Lorentz Group be constructed? If yes, how?
Note: Doug Sweetser has produced a Quaternion representation of the Lorentz Group, but he defined a new Norm to do so. Is the old Norm still meaningful? More information about this representation can be found at stackexchange.com, Is this a quaternion Lorentz Boost? Does any new representation of the Lorentz Group require the construction of a new Quaternion norm?
Relation to the Mobius Group The restricted Lorentz group SO+(1, 3) is isomorphic to the Möbius group, which is, in turn, isomorphic to the projective special linear group PSL(2,C). It will be convenient to work at first with SL(2,C). This group consists of all two by two complex matrices with determinant one
We can write two by two Hermitian matrices in the form
This trick has the pleasant feature that
Therefore, we have identified the space of Hermitian matrices (which is four dimensional, as a real vector space) with Minkowski spacetime in such a way that the determinant of a Hermitian matrix is the squared length of the corresponding vector in Minkowski spacetime. But now SL(2,C) acts on the space of Hermitian matrices via
where P* is the Hermitian transpose of P, and this action preserves the determinant. Therefore, SL(2,C) acts on Minkowski spacetime by (linear) isometries. We have now constructed a homomorphism of Lie groups from SL(2,C) onto SO+(1,3), which we will call the spinor map. The kernel of the spinor map is the two element subgroup ±I. Therefore, the quotient group PSL(2,C) is isomorphic to SO+(1,3).
Question 6: Can the resemblance of this representation to the Quaternion matrix representation above provide a connection between the two groups? What is the nature of this connection (i.e. is it an isomorphism etc.)?
Note: Spinors are related to Quaternions (For example, see the Chapter on Spinors in GRAVITATION by Wheeler, Thorne, Misner)
The Spinor Connection
Any 2X2 Hermitian Matric can be expressed as a linear combination of the Pauli Matrices (complexified quaternions). If the determinant is required to equal 1, then this group of matrices represents the Lorentz Group. Spinors are defined as 2 component complex vectors that are transformed by such matrices. Spinors are related to 4 vectors such that, for any spinor, an equavalent 4-vector can be found. Therefore, there is is a relationship between quaternions and 4-Vectors
The following passages from Introduction to Tensors Spinors&Relativistic Wave Equations by E.M. Corson (availabe on Archive.org) illustrate this.
The Quaternion and Lorentz Lie Algebras
Finding representations (of the Lorentz Group)* (sic)
According to general representation theory of Lie groups, one first looks for the representations of the complexification of the Lie algebra of the Lorentz group. A convenient basis for the Lie algebra of the Lorentz group is given by the three generators of rotations Jk=εijkLij and the three generators of boosts Ki=L0i where i, j, and k run over the three spatial coordinates and ε is the Levi-Civita symbol for a three dimensional spatial slice of Minkowski space. Note that the three generators of rotations transform like components of a pseudovector J and the three generators of boosts transform like components of a vector K under the adjoint action of the spatial rotation subgroup.This motivates the following construction: first complexify, and then change basis to the components of A = (J + i K)/2 and B = (J – i K)/2. In this basis, one checks that the components of A and B satisfy separately the commutation relations of the Lie algebra su2 and moreover that they commute with each other. In other words, one has the isomorphismThe utility of this isomorphism comes from the fact that su2 is the complexification of the rotation algebra, and so its irreducible representations correspond to the well-known representations of the spatial rotation group; for each j in ½Z, one has the (2j+1)-dimensional spin-j representation spanned by the spherical harmonics with j as the highest weight. Thus the finite dimensional irreducible representations of the Lorentz group are simply given by an ordered pair of half-integers (m,n) which fix representations of the subalgebra spanned by the components of A and B respectively....
Common representations(0,0) the Lorentz scalar representation. This representation is carried by relativistic scalar field theories.
(1/2,0) is the left-handed Weyl spinor and (0,1/2) is the right-handed Weyl spinor representation.
(1/2,0) ⊕ (0,1/2) is the bispinor representation (see also Dirac spinor).
(1/2,1/2) is the four-vector representation. The electromagnetic vector potential lives in this rep. It is a 1-form field.
(1,0) is the self-dual 2-form field representation and (0,1) is the anti-self-dual 2-form field representation.
(1,0) ⊕ (0,1) is the representation of a parity invariant 2-form field. The electromagnetic field tensor transforms under this representation.
(1,1/2) ⊕ (1/2,1) is the Rarita-Schwinger field representation.
(1,1) is the spin-2 representation of the traceless metric tensor.
-Wikipedia. Representation Theory of the Lorentz Group
Also, see the answer to How do I construct the SU(2) representation of the Lorentz Group using (the complexifection of)* SU(2)×SU(2)∼SO(3,1)? on physics.stackexchange.com. (*correction)
That is alot of information in a short space. The idea is to note that Quaternions are respresented by the complexification of SU(2) (or the and the Lorentz Group is represented by
Question 7: The complexified Pauli Matrices obey the Quaternion Algebra and generate SU(2). SU(2)XSU(2) generates the Lorentz Group. Can Quaternions be related to the same 4D (or (1/2,1/2) representation of the Lorentz Group in another way? In general, can multiple nonequivalent and irreducible representations represent a single (m,n) representation? In other words, can we use the theory of Lie Algebras to exclude the possibility of new and nonequivalent low dimensional Quaternion representations of the Lorentz Group? How are larger representations produced and evaluated?
Note: Similarity Transforms on the generators of the Lie Algebra (the Pauli Matrices) preserve the algebra of the generators.