Deflection and Scatter

When I started writing this blog, I wasn't sure about its direction, so I began by presenting something that I was curious about and hoped that others would find it interesting, while attempting to explain it would further my understanding. So I presented a classic derivation and asked for comments. The comments informed the second blog and made it much better than it would have been. I think this is a nice format. So, in this blog, I will present another classic derivation and ask the readers some questions about it, and, I'll try to ask a few questions relating to more modern developments in physics like String Theory.
General Relativity

This article contains some elementary mathematics. The format of the tutorial section of this article is structured such that the mathematical definitions are presented first, but don't be alarmed if you aren't familiar with the mathematics, they are followed by simple examples that demonstrate that the meaning of the mathematics and, hopefully, show that the mathematics isn't really that difficult. In fact, the mathematics makes the solution of the problem easier, not harder.

Mathematical Toolkit
A.The Derivative of a function
B.Tensors

Space and Geodesics: The precession of the perihelion of Mercury

The Principle of Equivalence: Gravitational Deflection of Light

A.The Derivative
For the purposes of this blog, the only idea from calculus I need is the idea of a derivative. If you've taken high school level math, you probably recall the slope of a line, that is merely the ratio of the change in y over the change in x, for a given change in x.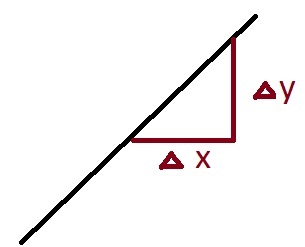

The slope of the line y=m(x-x_0)+y_0 is given by y-y_0/x-x_0=m

The derivative is the generalization of the idea of the slope to arbitrary, smooth, curves like y=x^2, y=x^5+x+a, e^x, log(x) and functions composed of these like x^2*e^x.

But, the slope of a curve generally isn't well defined because, unlike the case of a line, the slope of a curve varies.

The slope of the parabola y=x^2 increases as x increases, in other words, the slope is a function of x. The parabola doesn't have one slope. It has an infinite number of slopes. It has a different slope at each point.

Another issue with applying the idea of slope to a curve is that each point has a number of different slopes, depending on your choice of \delta x.

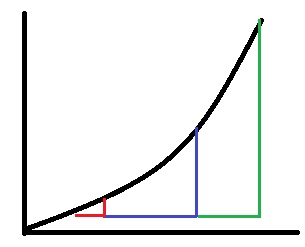
Rather than attempt to explain, in general, how the derivative resolves these issues, I will show how the derivative resolves both these issues by stating the definition of the derivative of a function and applying it to the case of a parabola.

Here is the definition of the derivative of f(x)

Begin by ignoring .

Example Calculation: The Derivative of x^2

Note that if , then by substitution, and

Now

is simply the value that

approaches as \Delta x approaches 0.

The derivative of y=x^2 is 2x.

1. Notice that the derivative is a function of x. It gives larger values for larger values of x. Well behaved functions have one derivative that has an infinite number of values. It gives the at each point.

2. The derivative is uniquely defined. There is only one value of f'(x) for each point x.

You can , roughly, think of the derivative as the "instanteous slope at a point"

B. Tensors

Now that you know what a derivative is I can introduce Tensors.

A Rank 1 Tensor is something that transforms according to