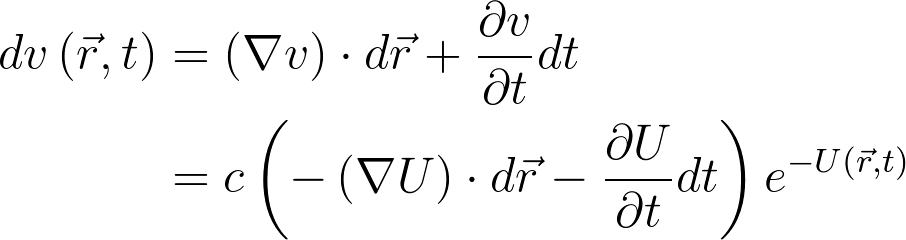Just a placeholder
and another
H1
H2
H3
H4
H5
H6
Just regular text
V(\mathbf{x})=-\int_{\mathbb{R}^3}\frac{G\rho (\mathbf{r})}{\left|\mathbf{x}-\mathbf{r} \right|}dv(\mathbf{r})
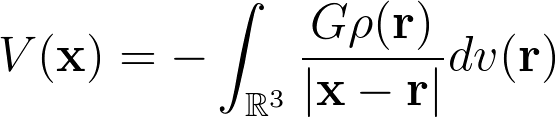
V(\mathbf{x})=-\int_{\Omega }\frac{G\rho (\mathbf{r})}{\left|\mathbf{x}-\mathbf{r} \right|}dv(\mathbf{r})
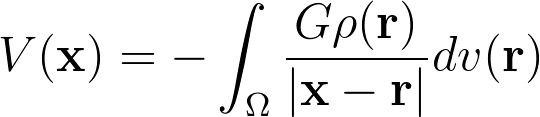
\mathbf{F}=\frac{d\mathbf{p}}{dt}
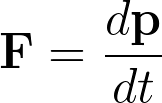
\mathbf{p}=m\mathbf{v}
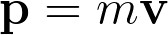
\frac{d\mathbf{p}}{dt}=\frac{dm\mathbf{v}}{dt}=m\frac{d\mathbf{v}}{dt}+\frac{dm}{dt}\mathbf{v}=m\mathbf{a}+\frac{dm}{dt}\mathbf{v}
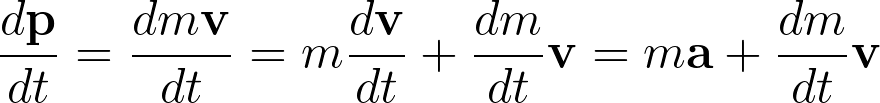
\mathbf{F}=m\mathbf{a}
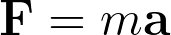
\frac{dm}{dt}\mathbf{v}=0
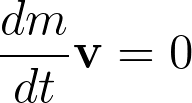
\frac{dm}{dt}=0
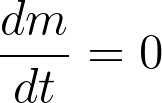
E_{ph}(r)
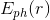
\frac{GM}{r^2}
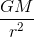
m_{ph}=\frac{E_{ph}(r)}{c^2}
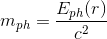
\frac{GM}{r^2}\frac{E_{ph}(r)}{c^2}
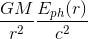
F_{G,ph}(r)=\frac{GM}{r^2}\frac{E_{ph}(r)}{c^2}
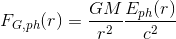
dE_{ph}=\frac{GM}{r^2}\frac{E_{ph}(r)}{c^2}\cdot dr
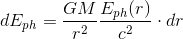
\vec{\nabla }E
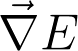

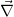
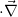
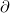
r=d\left(\vec{r}_o,\vec{r}_i \right)=\left|\vec{r}_o-\vec{r}_i\right|

U\left(\vec{r},t\right)=\frac{1}{F_{max}}\int_{\mathbb{R}^3}\frac{e\left(\vec{r}', t\right)}{d\left(\vec{r},\vec{r}'\right)}dv\left(\vec{r}'\right)
e\left(\vec{r}', t\right)


dv\left(\vec{r}\right)

\left(\epsilon_1 \mathrm{\: and\:} \mu_1\right)= \left(\epsilon_0 \mathrm{\: and\:} \mu_0\right)f\left(U\left(\vec{r},t\right)\right)

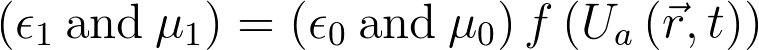
\begin{align*}
\left(\epsilon_2 \mathrm{\: and\:} \mu_2\right) &= \left(\epsilon_1 \mathrm{\: and\:} \mu_1\right)f\left(U_a\left(\vec{r},t\right)\right)\\
&= \left(\epsilon_0 \mathrm{\: and\:} \mu_0\right)f\left(U_a\left(\vec{r},t\right)\right)^2
\end{align*}
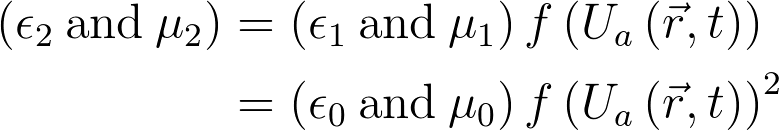
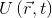
f\left(2U\left(\vec{r},t\right)\right)=f\left(U\left(\vec{r},t\right)\right)^2

\ln\left(f\left(2U\left(\vec{r},t\right)\right)\right)=2\ln\left(f\left(U\left(\vec{r},t\right)\right)\right)

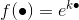
v\left(\vec{r},t\right)=ce^{-U\left(\vec{r},t\right)}
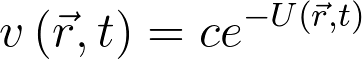
\epsilon\left(\vec{r},t\right)=\epsilon_0e^{U\left(\vec{r},t\right)}
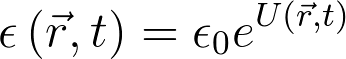
\mu\left(\vec{r},t\right)=\mu_0e^{U\left(\vec{r},t\right)}
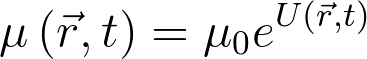
\begin{align*}
dv\left(\vec{r},t\right) &= \left(\nabla v\right)\cdot d\vec{r} + \frac{\partial v}{\partial t}dt\\
&= c\left(-\left(\nabla U\right)\cdot d\vec{r} - \frac{\partial U}{\partial t}dt\right)e^{-U\left(\vec{r},t\right)}
\end{align*}