Mathematics
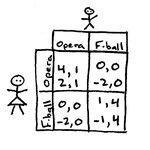
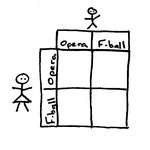
Yesterday, I posted Game Theory's El Farol Bar problem, with a couple questions. (If you haven't read it yet, go back—the answer's no good without the puzzle.) And the truth is there's no answer, or more precisely, there's no pure strategy that works—if everyone decides to go, the bar's too crowded and it's no fun; if everyone decides to stay home, the bar will be empty and it would've been more fun to go.
And so the best strategy is a mixed strategy in which each person has a set probability of going. The probability depends on how many people are deciding, the capacity of the bar, and how…
Think you're no good at Chess? Not a strategic thinker? You're better at it than you may think.
When we make any decisions related to how we think someone else will act, we must use reason to infer the other's next moves to decide what we must do. This recursive reasoning ability in humans has been thought to be somewhat limited but new research says people can engage in much higher levels of recursive reasoning than was previously thought.
Decision-making is part of day-to-day life, but when it involves competition, the complexity grows exponentially. Think of the…
Everyone loves the El Farol Bar in Santa Fe, New Mexico (especially W. Brian Arthur, who wrote this puzzle in 1994).
That is, everyone loves the El Farol as long as it's not too crowded.
If it's less than 60% full, it's more fun to be at the bar; if it's more than 60% full, it's more fun to stay home. This puzzle has one more catch: everyone has to decide whether or not to go at exactly the same time, without communication.
So what should you do—stay home or go to the bar?
You can probably see the Catch 22 here.
So rather than asking if you should stay home or go to the bar, a more precise…
vongehr |
Israel’s national lottery is all over the news these days because the same numbers (13, 14, 26, 32, 33, and 36) came up twice during one month.
A journalist called an expert on gambling, Z. Gilula, a professor of statistics in Israel, and asked him about the probability of the same set of numbers being randomly picked twice.They draw 6 numbers out of 37, thus there are 37!/(31! 6!) = 2324784 different possible drawings. Therefore, the probability of any one set of six numbers is p = 1/2324784 = 4.30 * 10-7. To get this twice in a row, you need to square it, i.e. the probability is really…
A numerical model can't help you finish a marathon, that will take a lot of running, but math can at least help you be the most efficient your body can be.
The best part about the night before a marathon is 'carb'ing up' the night before with a healthy pasta dinner but marathoners in training long before that make many mistakes with their diet, assuming "I'm in training" means they can eat twice as much of anything.
The best marathoners know the right fueling strategy is crucial and one dedicated marathoner, an MD/PhD student in the Harvard-MIT Division of Health Sciences and Technology…
Benoit Mandelbrot died on 14 October 2010 in a hospice in Cambridge, Massachusetts, at the age of 85. His name is synonymous with the study of fractals, a term he himself coined in the 1970s.
Fractals: Form, Chance and Dimension was published in English in 1977 (the original French came out two years earlier) but the book that sealed Mandelbrot's fame as an original thinker was the 1982 classic, The Fractal Geometry of Nature. It is one of those rare books that can be read both by professionals and lay readers. It also helps that it is copiously illustrated so that even if the mathematics…
Yesterday I posted how Game Theory solves the date-night dilemma: opera or the football game. Actually, I posted the problem but not the solution. For all of you who scratched your heads on Saturday night, here's the answer:
Mathematically, the cleanest solution is for them to use a commonly observed randomizing device: they flip a coin. Heads it's football and tails it's opera. And once the coin lands, there's no incentive for one player to switch, as it would only result in the loving husband and wife going separate ways for the evening and the loss of all preference points.
Actually,…
Can't decide between the opera and a football game? (If needed, replace these bland stereotypes with specifics from your own relationship). Game Theory's got your back.
Imagine the possible outcomes: football together, football alone, opera together, and opera alone. We can show this with the following grid (imagine the guy choosing a column and the lady choosing a row—they accept the outcome that gets two marks):Now imagine each person has five "preference points" they can distribute among the four outcomes (again: football together, football alone, opera together, opera alone). And imagine…
Hank |
When thousands of e-mails were obtained from the Climatic Research Unit (CRU) at the University of East Anglia in Norwich, UK, last year, global warming skeptics jumped all over the documents for signs that researchers had manipulated data. They hadn't (though their efforts to prevent anyone from obtaining the data, and the blowback from that, were as much cause for concern as the way in which hackers obtained them) but some of the e-mails discussed a different problem:
a CRU employee named "Harry", who often wrote of his wrestling matches with wonky computer software."Yup, my awful…
In the wake of blackouts across Italy in 2003 and that same year in the US northeast, two recent studies caused a Congress that has usually been preoccupied with important things like a law that will limit TV commercial volume to berate the energy industry because a military analyst worried that an attack on a small, unimportant part of the U.S. power grid might, like dominoes, bring the whole grid down.
The papers they used as evidence, one in Safety Science and one in Nature, are part of a growing reliance on a particular kind of numerical model, a topological model, for understanding…