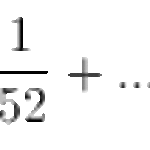Mathematics
It isn’t Monday, but I’m puzzled every day of the week.
Alice is puzzled too; she’s playing with a new tetrahedral die. Each face has a different positive integer on it, but the numbers are peculiar. Alice quickly notices that if she rolls the die and adds up the numbers on the three exposed faces, she always comes up with a perfect square. “That’s clever!” thinks Alice.
Assuming that Alice’s tetrahedral die uses the smallest possible numbers, what is the sum of the numbers on all four faces?
After the scramble to get out of jail, here are some questions about imprisoned shapes!
In my last question, we came across parts of the so-called harmonic series 1/2 + 1/3 + 1/4 + 1/5 ... 1/n. Now, this series is divergent; it does so very slowly, but as n tends towards infinity so does the sum. However, the sum of the squares of each term is convergent.
So, numerically, if we add together the areas of squares with sides of 1/2 units, 1/3 units and so on, we will tend towards a finite limit. However, is it possible to geometrically fit these squares inside a square of 1 unit side without…
The solution to the Jailer’s Revenge question is fairly lengthy, so I think it warrants a separate blog entry. Please refer to the original question as it too is fairly long.
Let’s firstly simplify the problem with smaller numbers, then scale it back up to 100 lockers and 100 prisoners. Let’s start with just 10 lockers and 10 prisoners.
The physical situation is unimportant; this is not a situational puzzle but a mathematical one. Indeed, there are variations on the scenario, such as putting people’s wallets in lockers. What is important is that the lockers and the prisoners are put into a…
A model based on global population data spanning the years from 1900 to 2010 has caused a research team to predict the opposite of what Doomsday Prophets of the 1960s and beyond insisted would happen - the number of people on Earth will stabilize around the middle of the century and perhaps even start to decline.
The results coincide with the United Nation's downward estimates, which claim that by 2100 Earth's population will be 6.2 billion, if low fertility and birth rate continues on its current path, below the 7 billion we are at now.
The numerical model developed by a…
This is a fairly new problem, being traced back to as recently as 2003. However, it also has the kind of counter-intuitive solution that has made it a favourite on mathematical websites and forums. In its various retellings, it sometimes suffers from a lack of stringent conditions that result in rather imaginative solutions; perfectly legitimate solutions within the parameters set but not always the ‘classic’ one. If you’ve seen this before, then speed-read to the end where we take the side of the jailer!
The problem
A jailer with too much time on his hands and a predilection for macabre…
The diagram below shows five concentric circles constructed in such a way that the area of each annulus is equal to that of the central circle. Within the first annulus, a square has been constructed such that none of the points on the square lie outside the inner or outer radii of that ring.
For the first annulus, A(1), with radii r(1) and r(2), n=4 is the minimum value of n such that a regular n-gon lies wholly within or on the boundary of A(1).
Find the smallest value of n, such that a regular n-gon will not fall outside the annulus A(m) bounded by r(m) and r(m+1) for values of m = 2, 3…
Alice wants to play a game with Bill. She has just bought some new and rather strange dice. The average of each die is 3.5, just like a normal playing die, but the numbers on each face have an unfamiliar distribution.
Die P has the numbers 3, 3, 3, 3, 3, 6.Die Q has the numbers 2, 2, 2, 5, 5, 5.
The game itself is very simple: whoever rolls the highest total wins a sweet from the candy box. If the box becomes empty, the winner can take one from the other player’s pile.
Alice has the following plan. Firstly, she lets Bill select which die he wants to play with. If Bill selects die Q then Alice…
Let N be a non-zero natural number composed of n digits. Let us then both prepend and append the number 4 to create two new numbers, 4N and N4, that are both (n+1) digits long. For example, if N is 123, then we create two numbers: 4123 and 1234.
The question is to find the smallest value of N, such that the following equation holds true:
4N = 4*N4
Again, using the example above, this would require that 4123 = 4*1234. This is obviously not true, so N=123 is not a solution.
So, find the smallest value of N and its length n.
If that was too easy, can we generalise the problem? Let K be our…
The "Circles Stuck in a Triangle" problem I posted last week had a rather surprising solution to it. So much so that I had to rewrite the question so that text and diagrams made sense! So here is a complete solution to what ended up being two problems; similar but different.
The solution has three steps: firstly, we need to find the relationship between the three radii; then there is a bit of number theory to find explicit numbers for a and b; and finally, some trigonometry to calculate the area of the large triangle.
The c=4 case
I will firstly find the general equation that links a, b and c…
If you are in the northern parts of the US (and lots of Canada) you will soon have sap running - and that means maple syrup. You probably don't think about the physiological aspects of syrup production - nor should you, that is why you have Science 2.0.
But now you can learn about the mechanisms of sap exudation—processes that trigger pressure differences causing sap to flow— while you eat your pancakes. In a paper published in the SIAM Journal on Applied Mathematics, authors Maurizio Ceseri and John Stockie propose a mathematical model for the essential physiological processes that drive sap…