The velocity profile of thin disk galaxies is a riddle worth pondering. Studies have shown that the velocity of stars in a galaxy rise to a peak as one leaves the center, and then stays flat as one looks further from the center. Newtonian gravitational theory can predict the peak correctly, but there must always be a decline.
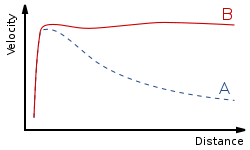
From Galaxy rotation curve, with A being the Newtonian prediction and B the data.
There are two parts to any force law: the cause and the effect. Consider the elliptical motion of the Moon around the Earth. The cause is the gravitational field of the Earth acting like a point source. The effect is the motion of the Moon around the Earth.
The rules of algebra allow one to cancel the mass of the Moon on both sides. It was Einstein who appreciated the depth of that step, the equivalence of gravitational and inertial masses. One can spot a core message of general relativity in this classical context. How much the Moon weighs is not relevant to its own gravitational motion. Gravity demands all masses orbit this way due to the Earth's gravitational field.
One can solve this equation to get the circular velocity:
Both G and the mass of the Earth are fixed numbers. Go out a larger distance and the velocity must drop. While the equation for a potential is quite different for a disk galaxy, the fact remains that the circular velocity must fall with distance.
There are two proposals to fix this issue that have received much research attention. The first is Modification Of Newtonian Dynamics, or MOND. When gravitational fields are weak, some ten orders of magnitude smaller than the acceleration of gravity on the surface of the Earth, then the form of the force law changes from a one over distance squared to one over distance. The proposal works great for the rotation profile of galaxies, closely matching over a hundred cases. MOND also does well with the Tully-Fisher relation. For even larger scales such as clusters of galaxies, MOND is not as successful. See The MOND Pages for a decent appraisal of the research.
Dark matter is another proposal that tries to solve the riddle. Here one modifies the cause to include enough dark matter to produce the velocity curves that are seen. The proposal does not work so well for the rotation profile of galaxies because there are few constraints on the distribution of dark matter in space. Dark matter is viewed as being quite a useful hypothesis for cosmology. A significant problem is that many dark matter candidates have been considered and rejected. Dark matter appears as the only player that can explain the weak gravitational lensing happening as a bullet cluster passes through another. In MOND, the gravitational and inertial masses must be exactly on top of each other. Yet the data says otherwise, the matter we see is in a different place from the gravitational potential. That is possible with dark matter.
The light matter proposal starts from the simplest observation: galaxies emit light. They do so by converting mass into photons. We need to account for this mass change somewhere in our velocity profile equation. While the amount of mass that gets consumed by fusion is exceptionally small, the change in the form of the velocity profile equation needs to be investigated.
Now consider the Earth in an elliptical orbit around the Sun. The numbers will change, but much of the math remains the same. A difference is that the Sun undergoes fusion, where two hydrogen atoms fuse to create one helium atom. Because the rest mass of the two hydrogen atoms is more than one helium atom, the mass decrease according to Einstein's most famous equation - E=m c2 - releases an enormous amount of energy. About 4 billion kilograms of mass are converted to various forms of energy per second. While that may sound huge, in the context of the Sun such a mass is not. The mass of the Sun is more than twenty orders of magnitude larger.
The gravitational potential of the Sun can be split into two components: the bulk which does not change in time, and the mass that does change in time due to fusion. Because these two masses enter as a sum into the potential, we can treat the Sun's mass as a constant. We cannot measure rotational speeds of planets to over ten significant digits, so the detail about fusion gets lost.
Finally, consider the rotation of stars in a thin disk galaxy. A number of things change. First, the source can no longer be viewed as a point. The potential function is no longer just the mass over the distance. The math problem was tackled in the 1960s by Alar Toomre using elliptical integrals. Later techniques used modified Bessel functions. With modern symbolic math programs, the rotation profile of a disk galaxy can be calculated by a computer in less time than it takes to type in the expression. Even with the fancier potential, a decline in velocity as the distance from the center of the galaxy remains unavoidable, yet inconsistent with observation.
Another change is that fusion happens for the masses effected by the force of gravity. All forces are a change in momentum, the product of mass times velocity. By the product rule of calculus:
The first term is the well-known mass times acceleration. The second term is the stuff of rocket science. Rockets are launched in a particular direction, and that is the direction of this term.
How would stars undergoing fusion contribute to this term? The photons go out in every direction, so when everything is even, there is no direction. A star is not a rocket.
Let's review why circular motion leads to the centripetal force that points radially. The velocity is perpendicular to the radius (see figure 2a).

Momentum is the product of mass times velocity, so at a time t, the momentum is perpendicular to the radius. A short time dt later, the star has moved along an elliptical path, retaining its momentum perpendicular to the radius. It is the direction of momentum that has changed. The only way to change momentum is through a force. The re-directional force points along the radius. The centripetal force of moving along an elliptical path is exactly balanced by the gravitational force from other stars in the galaxy.
For a star undergoing fusion in an elliptical orbit, the mass being held in orbit decreases (see figure 2b). As a star loses mass, it takes less force to keep it in place. Would that translate into the star going faster? Consider a speed skater with several weights going around a corner. The skater is doing everything he can to stay on the path. He lets go of weights in the turn. He works just as hard as before, but can now go faster because he weighs less.
The next step in solving the riddle is to determine what function one needs to use for the change in mass per unit of time. Start by defining a value for the fusion rate at the center of the galaxy: