[The article below is courtesy Eilam Gross. Eilam is a physicist from the ATLAS experiment and has been convener of the Higgs group there. I am very happy to host a guest post from him on the exciting topic below...]
It’s been three years
since the discovery of the Higgs Boson with the Large Hadron Collider (LHC) in
Geneva. Two beams of protons are accelerated to speeds approaching the speed of
light and colliding with energy densities similar to those existed fractions of
a second after the big bang. The discovery of the Higgs Boson filled in the
last vacancy in the Standard Model puzzle. All the particles predicted by the
Standard Model have been discovered, including photons, electrons, neutrinos
and quarks. Alas, this seemingly complete puzzle has not made Physicists happy.
Its foundations seem not to be on a solid ground. The model does not predict
the masses of matter particles, and we do not understand the hierarchy of the
particle masses, i.e. why some of them are so much heavier than others with
unnatural differences.
Physicists invented models that extend the Standard
Model and sort out some of its problems. These models, such as Supersymmetry,
contain more particles, most of them very heavy. Experimentalists turned their
attention to the search for heavy particles (including heavier Higgs bosons).
However, to discover heavy particle you need to produce them. And to produce
heavy particles one must collide the protons with higher energies. Indeed,
after the Higgs discovery, the collision energy was doubled to 13 TeV, i.e.
13,000 times the mass of the proton.
Physicists hoped to observe a new
heavy particle that is predicted by one of their many models. But none expected
to see the unexpected… A particle that no existing model predicts as is. This
might be the reason that physicists find it hard to digest the new observation
and play it as low as possible to reduce the expectations.
There is also a
firm scientific basis to the lowering of the expectations and it is
scientifically called: “The Look Elsewhere Effect”.
When we
discovered the Higgs boson, nobody was surprised. The Standard Model predicted
it, and we were expecting it. And the Higgs appeared with its full glory.
Particles like the Higgs have a very short life time, after which they decay
and transform themselves into other particles. The Higgs has plenty of decay
modes, and it manifested itself in most of them, such has four electrons, two
photons and many more.
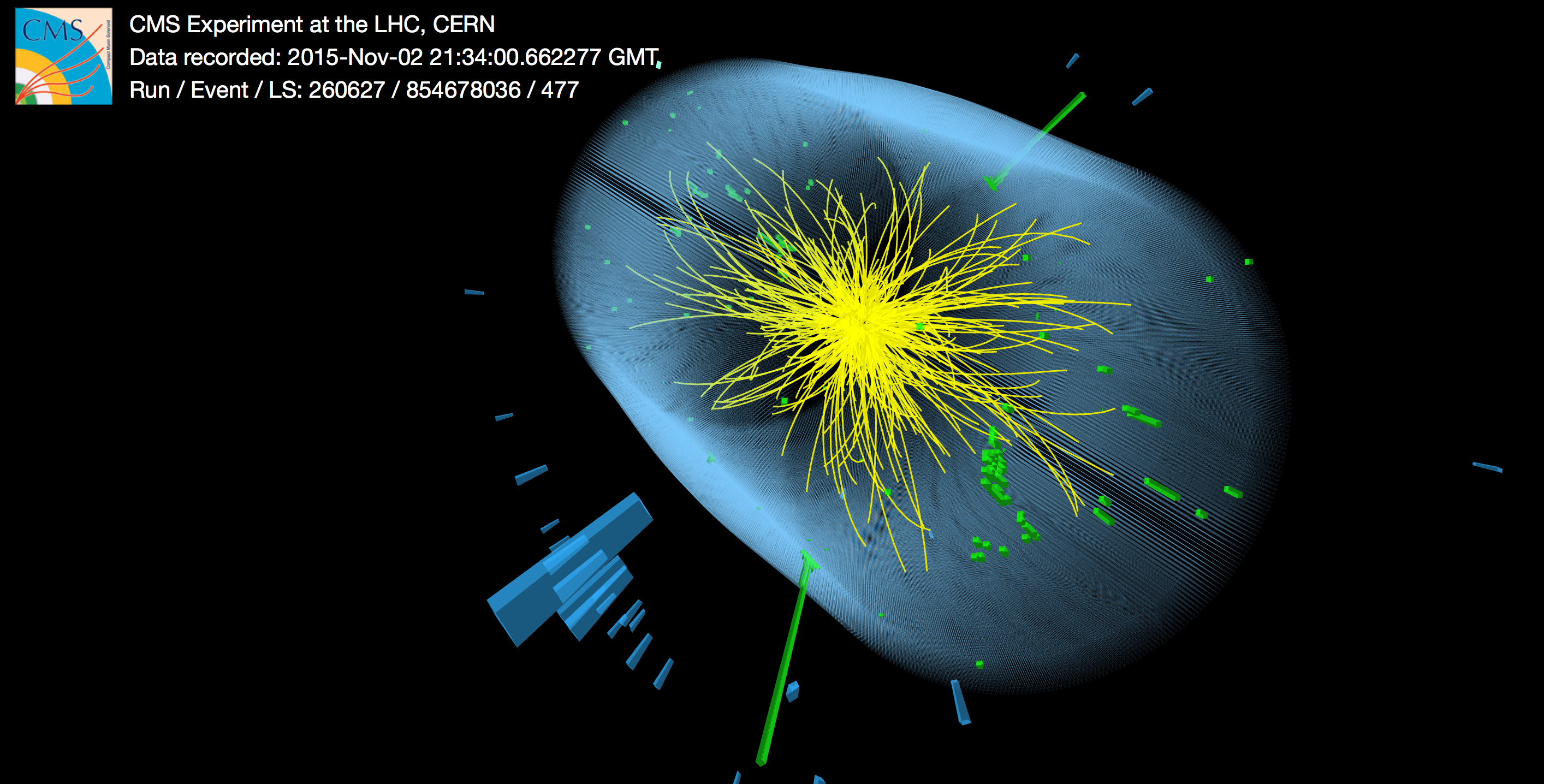
Figure 1 shows
one of the events which has generated the ongoing buzz. When one interprets the
diphoton, i.e. the two photons (green lines) as the remnants of a decay of a
heavier particle, one gets that the mass of that particle is 750 GeV, which
means, six times heavier than the Higgs boson. Had we seen only one particle
like this, we wouldn’t have got excited. The Standard
Model is predicting the existence of many collision events with diphoton masses
in that vicinity. However, we get many more, many more than predicted by the
Standard Model. So the only remaining question is how many more one needs to
observe in order to summon a press conference. The answer is given using a
statistical term called significance. A Significance is measured and expressed
by the number of standard deviations.
Let us
illustrate it with an example. A quick search in google reveals that the
average height of the American man is 177 cm with a standard deviation of 8 cm,
which means, that about 2/3 of the American male population are between 169-185
cm tall. Michael Jordan, however, is not in this range. He is 198 cm. This
means that his height is almost three standard deviations above the average.
Less than a quarter of a percent of the men in the USA are as high as Michael
Jordan or more. Shaquille O’neal is even taller. He is 216 cm, five standard
deviations above the average. Only about 30 men, out of 170 million American
men are as tall as this or taller. Which means that the probability that a
random American man will be as tall is less than one in a million. No doubt
that being five standard deviations above the average is extraordinary and
draws attention. There is no known American man who is six standard deviations
above the average height. If you see one like this walking down the street, you
will plausibly think its and alien, and would probably be right…
No wonder there
is a tradition amongst physicists that if in a collision, the number of
observed events with some specific mass, exceed that of the exception by more
than five standard deviations, this is probably not a result of a statistical
fluctuation of the expected known physical processes, but a newly discovered
particle. Five sigma, or 5 standard deviations, is the magic number used by
physicists to declare a discovery. Both LHC experiments, ATLAS and CMS,
reported in July 2012, an excess of events with a mass of 125 GeV exceeding the
five sigma expectation. They observed it in two decay modes, one of which was
diphotons. The probability of a mistake in each of the experiment was less than
one in a million. By a mistake, we mean that the observation IS a statistical
fluctuation and not a newly discovered particle. Since both experiments
observed it at the same mass, the confidence in the result was strong enough to
allow the CERN Director General Rolf Heuer to say his famous words: “As a
layman I would say, I think we have it”, in other words, the Higgs boson
has been discovered.
In seminars
given in Geneva on Tuesday 14 Dec 2015, both ATLAS and CMS reported an excess
of diphoton events with a mass of 750 GeV ( 6 times heavier than the Higgs
boson).
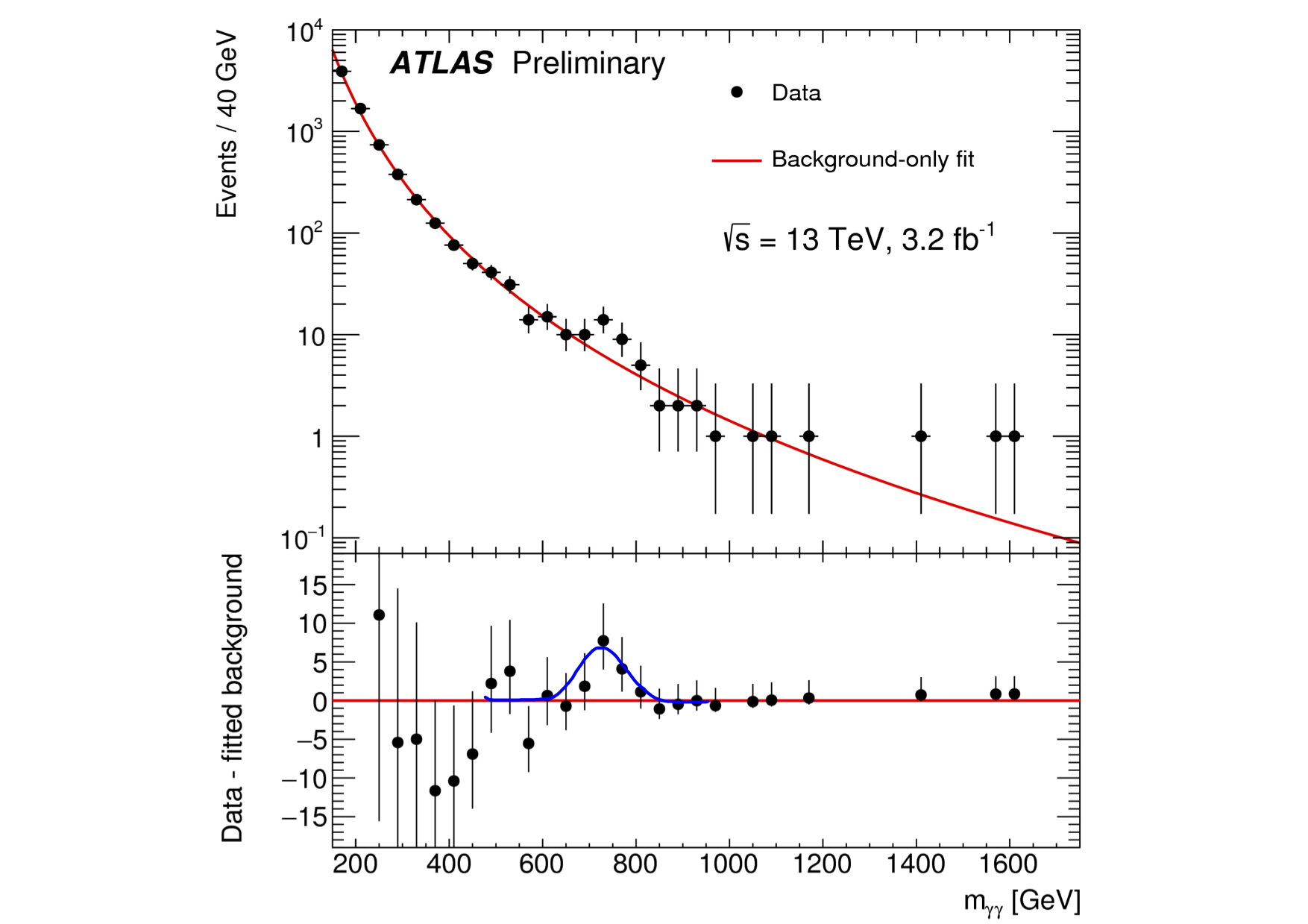
Figure Figure 2 shows
the distribution of the mass of diphoton events recorded by the ATLAS
experiments during 2015. We see there events with all possible masses from
200-1600 GeV. The red curve in the top part of the plot indicates the
expectation from the Standard Model. In some masses, we see an excess of events
and in some a deficit on the Standard Model expectation. The excess or deficit
is shown in the bottom part of the plot. One clearly sees an unusual clustering
of excessed events in the vicinity of 750 GeV. This clustering creates a bump
in the shape of a bell. To guide the eye, I plotted a blue bell (bottom of
Figure 2) which does not exist in the original plot from ATLAS. If one try to
match the bell to the excess of events and count the events inside the bell,
one gets that there are about 15 events on top of about 15 expected events (a
total of about 30 events). The probability of a statistical fluctuation of the
expected 15 events to give over 30 events is less than 1:10000, and is
equivalent to an almost, four sigma deviation from the expectation. In our American male population example, four
sigmas would be a man with a height exceeding 209 cm, given the average is 177
cm with a standard deviation of 8 cm.
Less than
1:10000 is a very low probability or,
alternatively, very high significance. So why didn’t ATLAS get
excited and call for an urgent press conference?
We will
discuss it now.
Note that in
the bottom part of Figure 2 there is an excess of events in other masses, not
only 750 GeV, There is an excess at 500,1400, 1600 GeV.
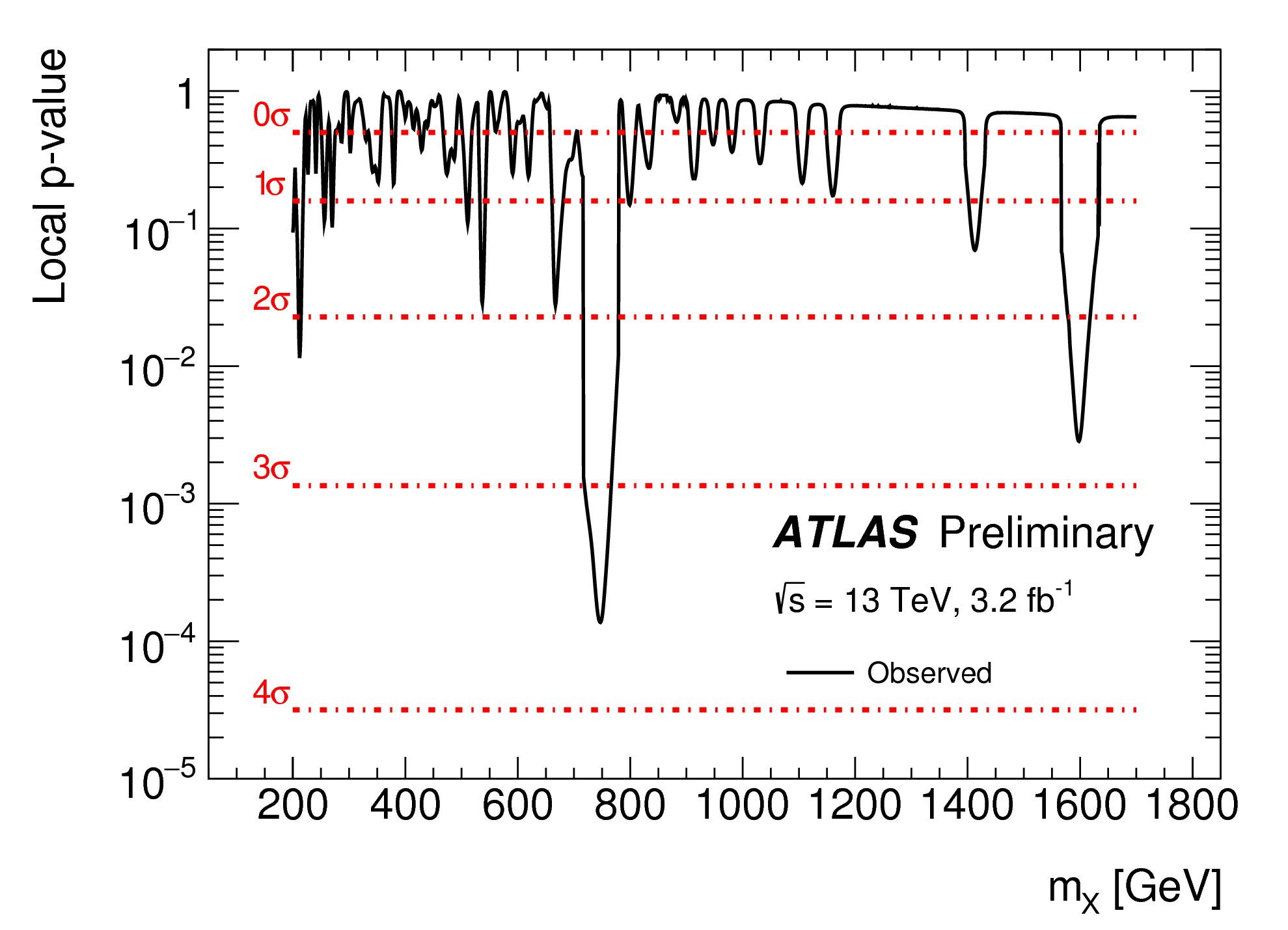
Figure 3 shows
the probability that the fluctuation we observe in a specific mass is a result
of a fluctuation of the Standard Model. One clearly sees that the smallest
probability occurs at 750 GeV. The lower the probability for a fluctuation is,
the higher is the significance, and it becomes more plausible to speculate a
new particle, i.e., the excess is not a fluctuation but a result of new
physics. At a mass of 750 GeV we see a four sigma excess, but there is also an
excess at the level of 3 sigmas at a mass of 1600 GeV. The plot shows many statistical fluctuations.
It turns out statistical fluctuations are a matter of routine, and one has to
take a lot of precaution before declaring that a significant excess is not a
fluctuation but evidence for a new particle.
When we said
that the probability to see a statistical fluctuation around a mass of 750 GeV
is less than 1:10000, we answered the following question: “What is the probability that the
expectation of 15 events with a definite mass of 750 GeV, will fluctuate to
give over 30 events at that mass?”.
Here we
require investing some more thought. Had we seen such am excess at any other
mass (not necessarily 750 GeV), we would have also cried “wolf,
wolf”. It would
have drawn our attention in the same manner. Had we seen it in 200, 300, 600,
1000, any other mass. There is nothing special a-priori in 750 GeV. This means
that we have not answered the right question. We should have asked: “What is the probability of seeing
an excess exceeding 4 sigma ANYWHERE in the search mass range”. This probability is certainly
bigger than the probability to see the excess at exactly 750 GeV. Higher
probability leads to a notable reduction of significance.
This effect of
degrading significance as a result of pausing a different question, of looking
everywhere in the search range, is called, “the Look Elsewhere Effect (LEE)”. Its calculation is very
complicated but formulas that are easy to use were derived. The LEE can also be extended to more than one
variable in action. For example, we can extend the question and ask, “
What is the probability of seeing
an excess exceeding 4 sigma with any mass and bell width in the search
mass-width range?”. This probability would even be higher. The effect is
called, “the multidimensional LEE”.
|
Figure 4:
|
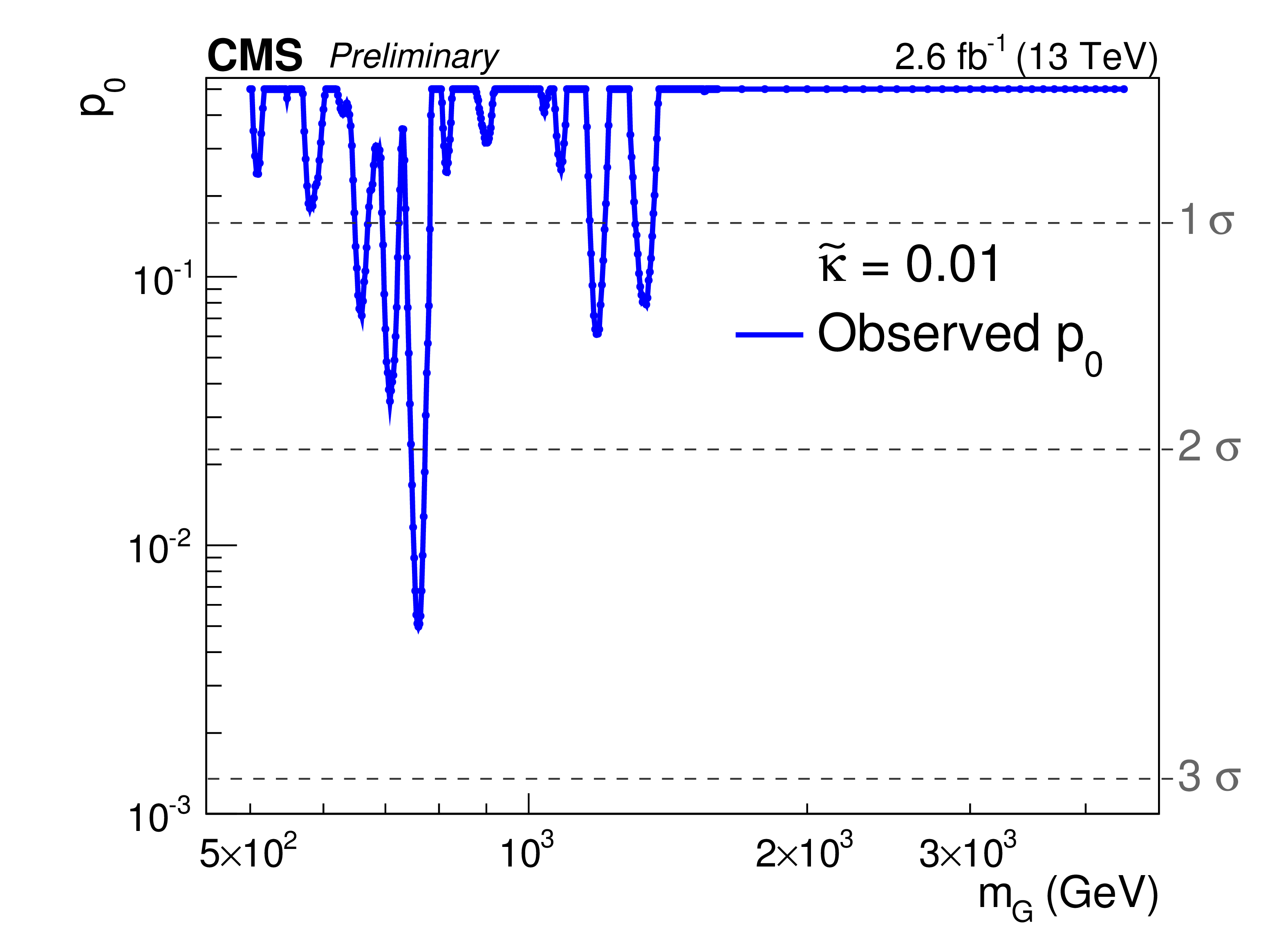
ATLAS,
therefore, answered the latter question: "what is the probability of
seeing an excess of over four sigmas, with any mass and bell width in the
search range?". In answering that, the significance degraded to 2.2 sigma,
which means, the probability to see a fluctuation as the one we see or bigger,
is 1.5%. This is considered a low probability. Two sigma fluctuations are very
common and frequent when we make hundreds if not thousands of measurements.
This is the reason ATLAS took their 750 GeV 4 sigma excess with a grain of salt
and played it extremely low.
You probably
wonder what CMS have observed at the same mass range.
Figure 4 shows
the probability for fluctuations at given masses as recorded by CMS in 2015.
The lowest probability occurs at 760 GeV and is equivalent to a significance of
2.6 sigmas. When one takes the Look Elsewhere Effect into account, this
probability is completely degraded and is becoming 1.2 sigma. One sigma
fluctuations are so frequent that no one pays any attention to them.
Nevertheless,
the very fact that BOTH experiments see the most significant excess around the
same mass (750-760 GeV), and the high significance of close to 4 sigmas
observed by ATLAS, generating lots of excitement in the High Energy Phenomenologists
community.
While I write
these lines, one day after the release of the results, there are already over
ten papers on the web. All of them trying to explain the unexpected excess and
why it prefers to decay to two photons, and not to anything else…. From one of them, by Buttazo et.
al. (“
Knocking on New Physics' door with
a Scalar Resonance”) I stole the title of this post.
Luckily for
us, we will know the answer in about half a year, when the accelerator that is
now in shutdown, will resume its operation in spring 2016. Until then the phenomenologists can continue
to dream and enjoy the doubt.
Bibliography:
1.
ATLAS note: ATLAS-CONF-2015-081 https://cds.cern.ch/record/2114853/files/ATLAS-CONF-2015-081.pdf
2.
CMS note: CMS-PAS-EXO-15-004
https://cds.cern.ch/record/2114808/files/EXO-15-004-pas.pdf
3.
1-D Look
Elsewhere Effect: Eilam Gross and Ofer Vitells, Trial factors for the look
elsewhere effect in high energy physics, Eur.Phys.J.C70:525-530,2010, http://arxiv.org/pdf/1005.1891v3.pdf
4.
Multidimensional
Look Elsewhere Effect: Ofer Vitells and Eilam Gross,Estimating the significance
of a signal in a multi-dimensional search, Astropart.Phys.
35 (2011) 230-234, http://arxiv.org/pdf/1105.4355.pdf
5.
Routines for
calculating the LEE based on the above papers: Kyle Cranmer, GitHub, https://github.com/cranmer/look-elsewhere-2d